避免根切的条件：齿面Σ2优化方案

由式（3-1）可知，θ是齿面Σ₁的参数，在过O₃垂直于齿轮1轴线的平面上，由Ψ=0得到式（3-62），求得许用最大值θ_max，当θ＞θ_max时齿面Σ₂出现根切。

1.插齿刀许用最大半径

由图3-5可以看到，齿轮2无根切时，插齿刀的许用最大齿顶圆半径r_aomax为

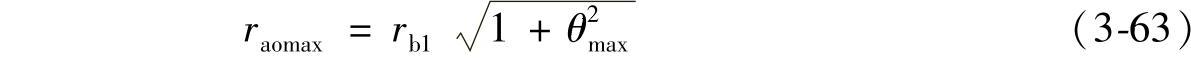
如果已经给定了插齿刀的齿顶圆半径r_ao，则可由下式求得θ_max为

再由式（3-62）求得Σ值，确定轴交角Σ的允许变动范围。

2.Σ=0时，避免根切的条件

通常以Σ=0为初步设计的参考。将Σ=0、α′=α代入式（3-56b）得曲率干涉界线函数为

式中，a₀≠0，α≠0，sinα≠0；Ψ₀=0的条件是

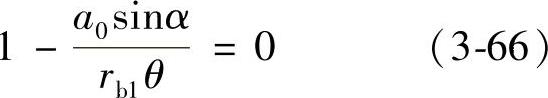
或者

c=r_b1（cosα+θsinα）-l₁=0 （3-67）

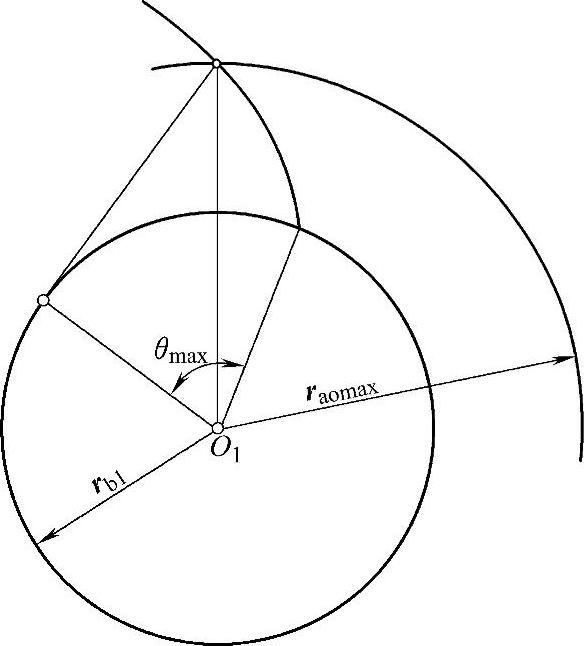
图3-5 插齿刀的许用最大齿顶圆半径

齿轮1齿面Σ₁的单位法矢量n₁由齿的实体指向空域时，由式（1-125）和式（1-126）得齿面Σ₂无曲率干涉的条件为

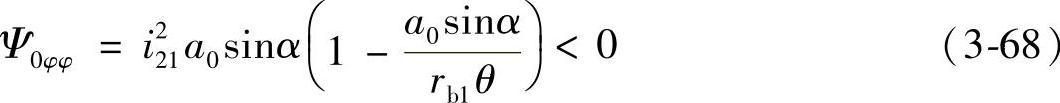
Ψ₀=Ψ_0φφcsinα＞0 （3-69）

（1）Σ=0时，插齿刀最大半径

由式（3-66）和式（3-68）得(www.xing528.com)

θ≤a₀sinα/r_b1

于是

θ_0max=a₀sinα/r_b1 （3-70）

将式（3-70）代入式（3-63），得到Σ=0时Σ₂无根切的插齿刀许用最大齿顶圆半径为

（2）轴线Ⅲ与轴线Ⅰ的最小轴间距

如图3-2所示，轴线Ⅰ与轴线Ⅲ公垂线的垂足分别为O₁和O₃，轴间距l₁=。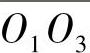

齿面Σ₂无曲率干涉的条件中，当要求Ψ_0φφ＜0时，式（3-69）中，只有c＜0才能保证Ψ₀＞0。由式（3-67）和c＜0得

c=r_b1（cosα+θsinα）-l₁≤0

由上式可得到轴间距l₁的许用最小值为

l₁Σ_min=r_b1（cosα+θ_asinα） （3-72）

式中 d_a1——齿轮1的顶圆直径。

式（3-72）中各参数的关系如图3-6所示。

当l₁＞l_1Σmin时，可以保证齿轮2的齿线向齿轮2轴线方向凹（见图3-7），不会与齿轮1齿面Σ₁干涉。

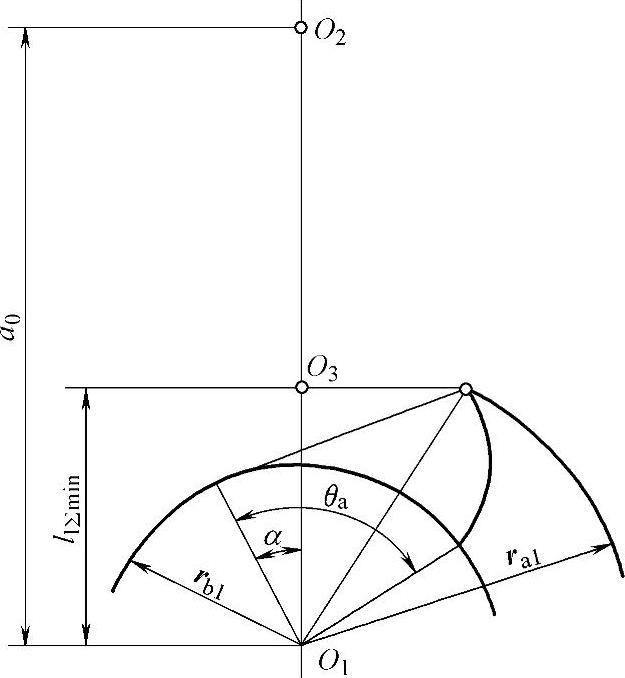
图3-6 l_1Σmin值与其他参数的关系

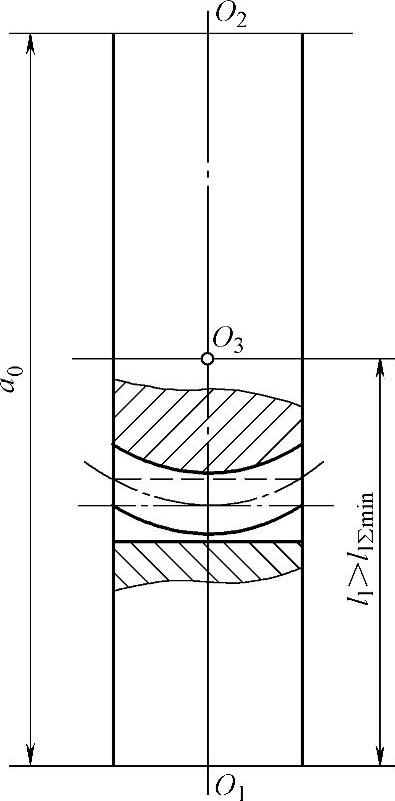
图3-7 齿线无干涉时的l₁值