啮合面方程与啮合角的关系

关于φ的共轭条件函数，由式（3-9）和式（3-22）得

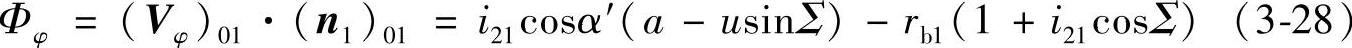
关于Σ的共轭条件函数，由式（3-9）和式（3-26）得

Φ_Σ =（V_Σ）₀₁·（n₁）₀₁=usinα′ （3-29）

关于Σ的共轭条件方程为Φ_Σ=0，由式（3-29）得

u=0

将u=0代入式（3-4）和式（3-28）。由式（3-4）和关于φ的共轭条件方程Φ_φ=0，得到在σ₀₁里的啮合面方程为

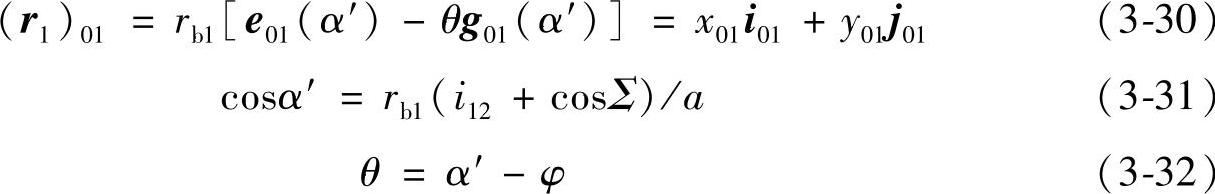
由式（3-30）可知，在σ₀₁里各接触点落在过轴心O₃、垂直于齿轮1轴线的平面上，此平面称为啮合平面。在σ₁里齿面Σ₁上u=0的渐开线齿廓为接触迹线。

当给定Σ值时，由式（3-31）求得啮合角α′，得到一条啮合直线（见图3-4）；给定齿轮1的转角φ时，由式（3-32）求得θ值，在啮合直线上得到接触点M。随着齿轮1转角φ的变化，点M在啮合直线上移动，同时在齿面Σ₁的渐开线齿廓上移动。轴交角Σ变化时，啮合角α′变化，|Σ|值越大，α′越小。在啮合平面上得到相切于齿轮1基圆的啮合直线族。(www.xing528.com)

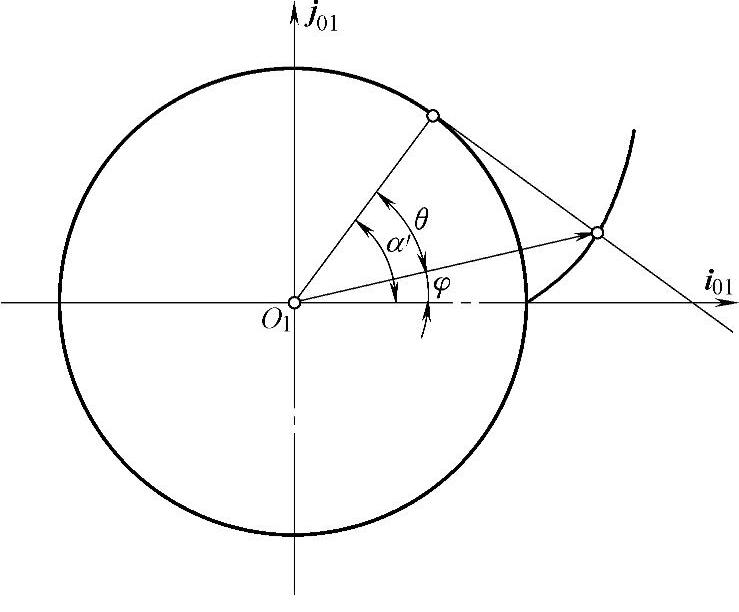
图3-4 Σ为定值时的啮合直线

当轴交角Σ=0°时，两轮轴线平行，其中心距为

a₀=l₁+l₂=r₁+r₂ （3-33）

式中 r₁——齿轮1分度圆半径；

r₂——齿轮2中截面分度圆半径。

由式（3-31）得

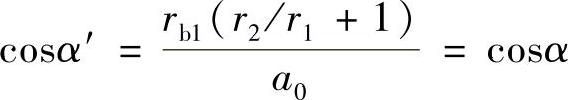
Σ=0°时，啮合角α′与齿轮1分度圆压力角α相等。