直齿渐开线圆柱齿轮齿面优化技巧

如图3-3所示，在坐标系σ₁里，使i₁轴过半径为r_b1的基圆上渐开线始点。利用圆矢量函数（见附录A），在σ₁里得到齿轮1的渐开线柱面Σ₁的方程为

（r₁）₁=r_b1e₁（θ）-r_b1θg₁（θ）+uk₁ （3-1）

式中，u、θ为渐开柱面Σ₁的参数。u为常数，得到渐开线齿廓（θ曲线）；θ为常数，得到渐开线柱面直母线（u直线）。由式（3-1），在σ₁里（r₁）₁的一阶偏导数为

（r_1u）1=k₁

（r_1θ）1=r_b1θe₁（θ）

Σ₁的第一类基本量为

E=（r_1u）₁·（r_1u）₁=1

F=（r_1u）₁·（r_1θ）₁=0

G=（r_b1θ）²

Σ₁的单位法矢量为

（n₁）1=（r_1u）1×（r_1θ）1/D=r_b1θg₁（θ）/D

令n₁由齿轮1齿的实体指向空域，D取负值，即

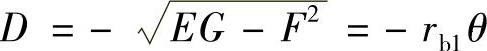
于是得到

（n₁）1=-g₁（θ） （3-2）

在σ₁里（r₁）₁的二阶偏导数为(www.xing528.com)

（r_1uu）₁=0

（r_1uθ）₁=0

（r_1θθ）₁=r_b1[e₁（θ）+θg₁（θ）]

Σ₂的第二类基本量为

L=（n₁）₁·（r_1uu）₁=0

M=（n₁）₁·（r_1uθ）₁=0

N=（n₁）₁·（r_1θθ）₁=-r_b1θ

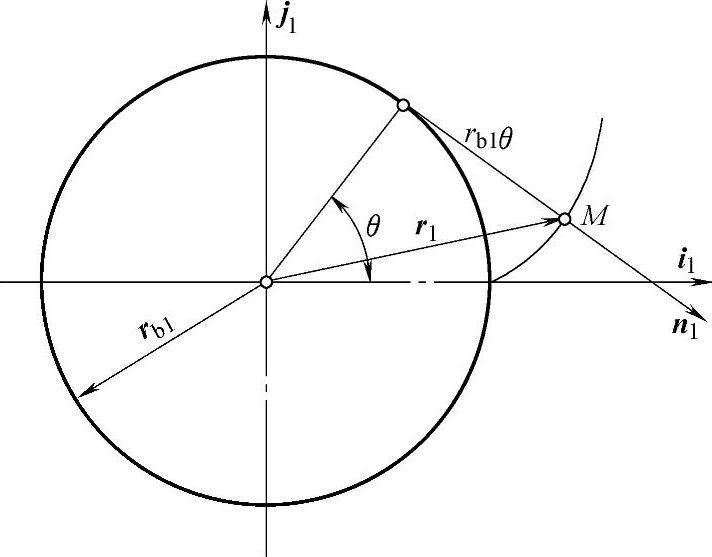
图3-3 渐开线起始点的位置

渐开柱面为可展直纹面，其参数曲线u方向和θ方向为主方向，其主曲率和短程挠率分别为

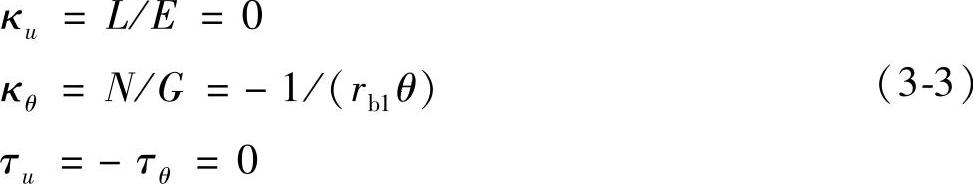
利用坐标变换单位矢量法（见附录B），将式（3-1）和式（3-2）进行σ₁→σ₀₁坐标变换，在σ₀₁里得到曲面族{Σ₁}₀₁的方程为

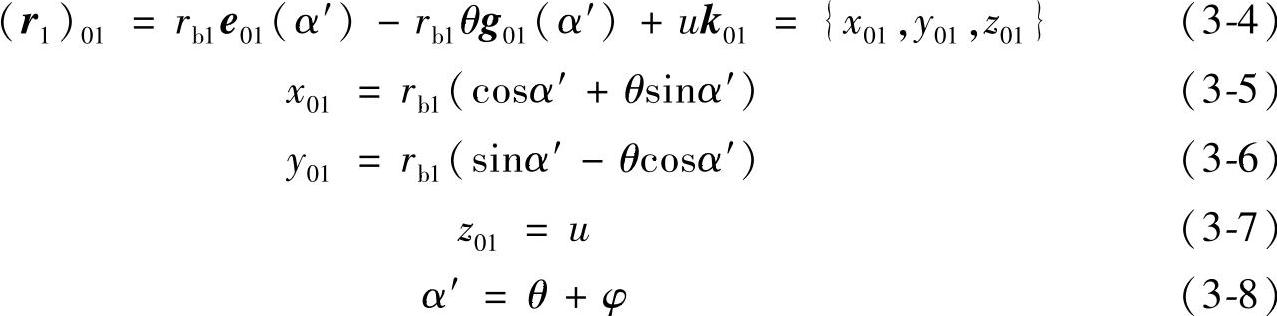
单位法矢量为

（n₁）₀₁=-g₀₁（α′） （3-9）