利用相对角速度Ωpiφ运动展成齿面Σi的优化方法

1.产形面族{Σ_p}_p的方程

图2-4所示起始位置φ=0，产形面的方程为式（2-159），将其绕k_p转过S_hφ角，在σ_p里得到产形面族{Σ_p}_p的方程为

{Σ_p}_p上活动标架的3个单位矢量为

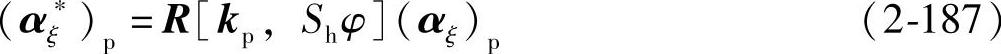
2.关于φ的相对角速度Ω_piφ

在σ_p里，由式（2-147）得

将式（2-191）代入式（2-190）得

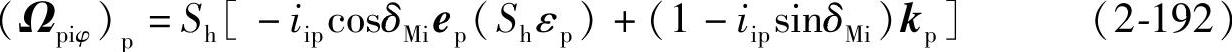
3.关于φ的相对速度V_piφ

在σ_p里关于φ的相对速度为

（V_piφ）_p=（Ω_piφ）_p×（r^∗_p）_p-（v_op）_p （2-193）

（v_op）_p=（ω_iφ）_p×（O_ip）_p （2-194）

由式（2-138）得

（ω_iφ）i=S_hi_ipk_i （2-195）

由图2-4得

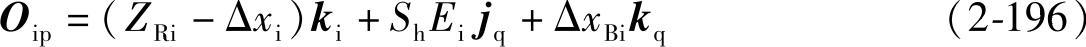
由式（2-194）、式（2-195）和式（2-196）得

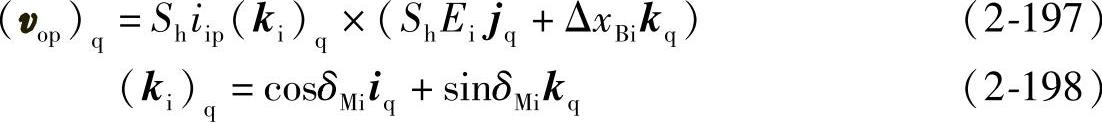
将式（2-198）代入式（2-197）得

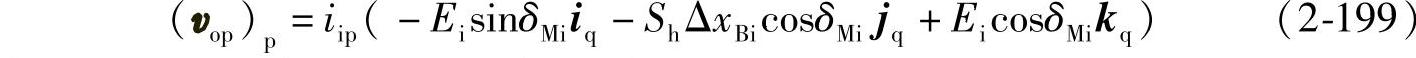
将式（2-199）进行σ_q→σ_p坐标变换得

4.切齿啮合共轭条件函数

产形面Σ_p与齿面Σ_i切齿啮合共轭条件函数为

Φ=V_piφ·n_p

将式（2-189）和式（2-193）代入上式得

(https://www.xing528.com)

Φ=0为切齿啮合共轭条件方程。

式（2-159）和Φ=0为产形面Σ_p上瞬时接触线方程。

式（2-186）和Φ=0为切齿啮合面在σ_p里的方程。

5.啮合界线函数

由式（2-186）和式（2-189），可将式（2-201）改写成

将式（2-202）对φ求偏导数，得切齿啮合界线函数为

式（2-159）和Φ=Φ_φ=0为产形面Σ_p上啮合界限方程。

6.产形面Σ_p上的接触线法矢

在σ_p里产形面族{Σ_p}_p中每一个产形面上的接触线法矢为

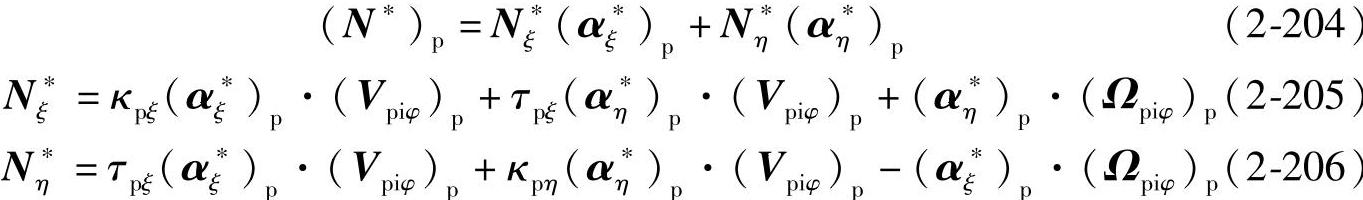
7.被展成齿面Σ_i的方程

对式（2-186）进行点的σ_p→σ_i坐标变换得

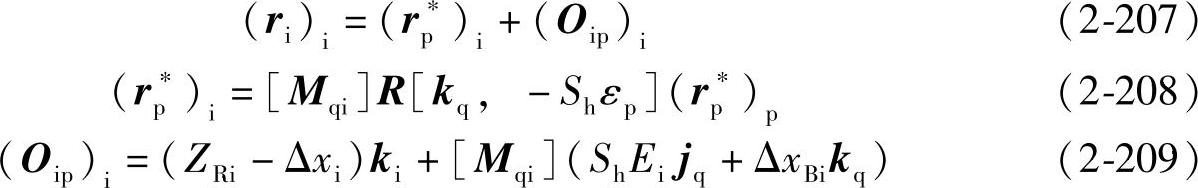
式（2-207）的矢量绕k_i反转S_hi_piφ角，在σ_i里得到产形面族{Σ_p}_i的方程为

式（2-210）和Φ=0为被展成齿面Σ_i的方程。

8.曲率干涉界线函数

切齿啮合曲率干涉界线函数为

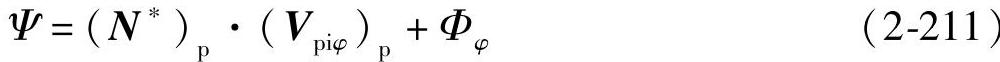
式（2-210）和Φ=Ψ=0为齿面Σ_i上曲率干涉界线方程。

9.齿面Σ_i的曲率参数

齿面Σ_i沿α_iξ=α^∗_ξ方向的法曲率为

短程挠率为

齿面Σ_i沿α_iη=α^∗_η方向的法曲率为