相对角速度运动形成产形面

1.产形面Σ_p的方程

图2-4所示起始位置φ_p=0（ψ=0，φ=0）。对式（2-150）进行点的σ_d→σ_p坐标变换，在σ_p里得

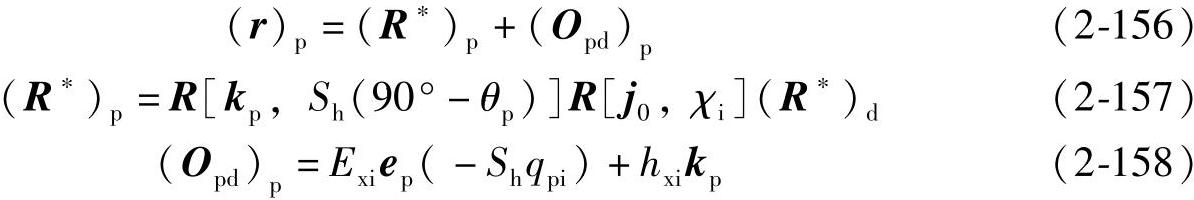
将矢量（r）p在σ_p里绕k_p反转S_hi_pdψ角，得到产形面Σ_p的方程为

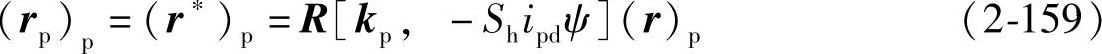
将式（2-156）代入式（2-159），化简后得到

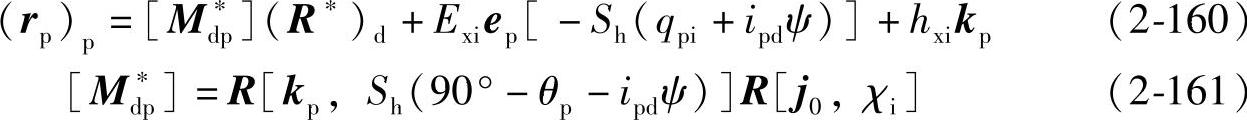
在σ_p里Σ_p的直母线Γ_d的单位矢量为

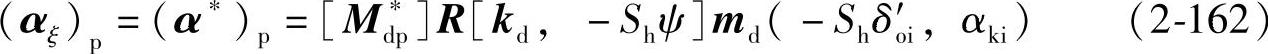
2.关于ψ的相对速度V^∗_dpψ

（1）关于ψ的相对角速度Ω^∗_dpψ

将式（2-143）进行σ_d→σ_p坐标变换，并绕k_p反转S_hi_pdψ角，得到关于ψ的相对角速度为

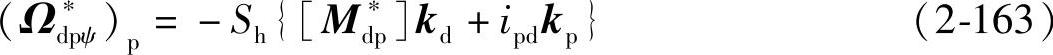
（2）关于ψ的相对速度V^∗_dpψ

在式（2-10）中，将下标1换成p，k换成ψ，考虑到O_pd为常矢，得

V_dpψ=Ω_dpψ×R-ω_pψ×O_pd （2-164）

R在σ_d里绕k_d回转，由式（2-150）得到（R^∗）_d；进行σ_d→σ_p坐标变换，由

式（2-157）得到（R^∗）_p；再绕k_p反转S_hi_pdψ角得

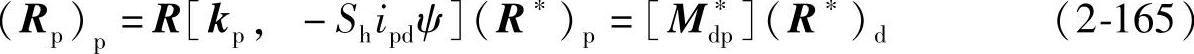
由式（2-137）得

（ω_pψ）p=S_hi_pdk_p （2-166）

由式（2-158）和式（2-166）得

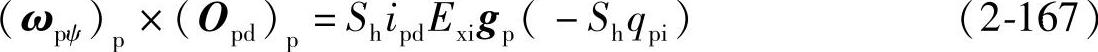
式（2-167）中矢量绕k_p反转S_ni_pdψ得

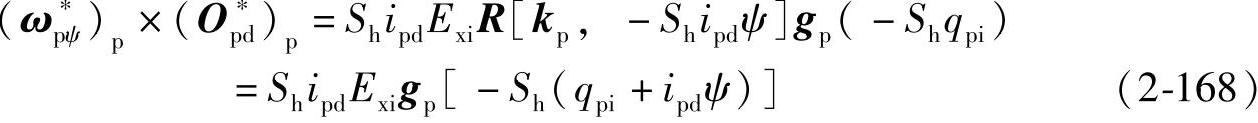
V_dpψ绕k_p反转S_hi_pdψ角，将式（2-163）、式（2-165）和式（2-168）代入式（2-164）得

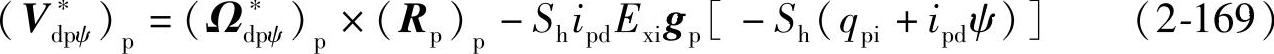
3.产形面Σ_p的单位法矢

轨迹曲面Σ_p上任一点处，刀刃直线Γ_d的单位矢量（α_ξ）_p和关于ψ的相对速度V^∗_dpψ，都在其切平面上，Σ_p的单位法矢为

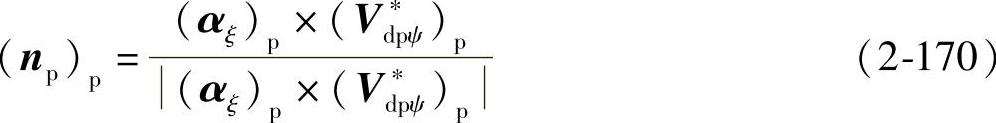
在Σ_p上任一点Q处取活动标架[Q；（α_ξ）_p，（α_η）_p，（n_p）_p]，其中

（α_η）_p=（n_p）_p×（α_ξ）_p （2-171）(https://www.xing528.com)

4.产形面Σ_p的曲率参数

利用本章2.4节方法计算轨迹曲面Σ_p的曲率参数。

（1）Σ_p沿α_ξ方向的法曲率和短程挠率

式（2-34）中代入直线Γ_d的曲率κ=0，得Σ_p沿α_ξ方向的法曲率为

κ_pξ=0

式（2-35）中代入κ_pξ=0，得Σ_p沿α_ξ方向的短程挠率为

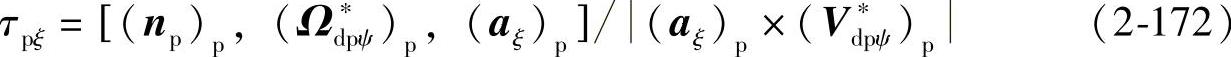
（2）Σ_p沿V^∗_dpψ方向的法曲率和短程挠率

现在不能用计算g的公式（2-31）代入式（2-37）来计算法曲率，需要由式（2-164）重新推导。O_pd和ω_pψ均为常矢，微分式（2-164）得

dV_dpψ=dΩ_dpψ×R-Ω_dpψ×dR （2-173）

dR=d_dR+（Ω_dpψ×R）dt （2-174）

将式（2-174）代入式（2-173）得

dV_dpψ=（Ω_dpψ×α）dS_d+gdt （2-175）

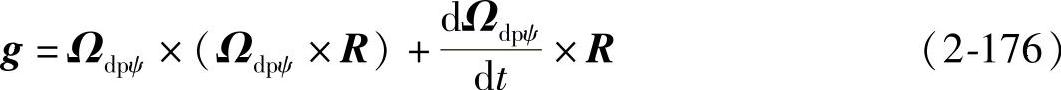
将式（2-163）和式（2-165）代入式（2-176），并考虑到d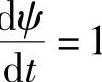，得

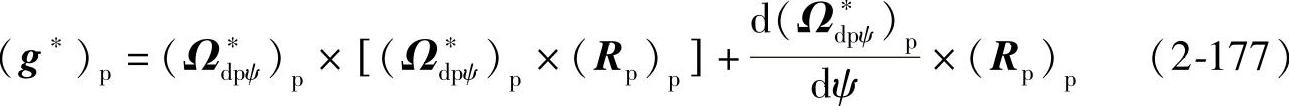
将式（2-163）对ψ求导得

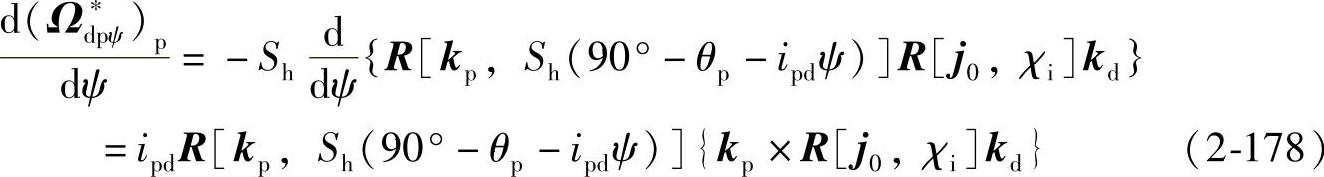
式（2-178）中

k_p×R[j₀，χ_i]k_d=k₀×R[j₀，χ_i]k_d=sinχ_ij₀ （2-179）

将式（2-179）代入式（2-178）得

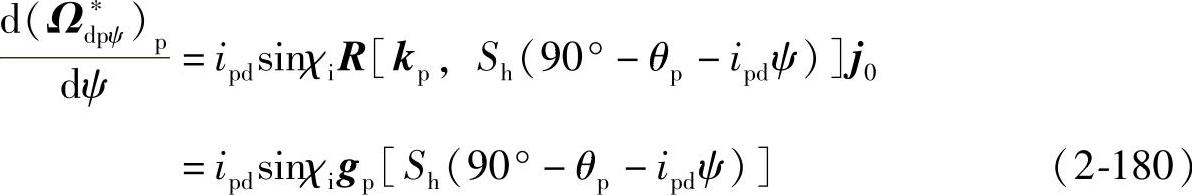
由式（2-37）得Σ_p沿V^∗_dpψ方向的法曲率为

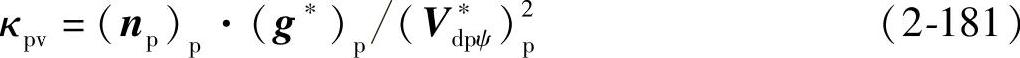
由式（2-38）得Σ_p沿V^∗_dpψ方向的短程挠率为

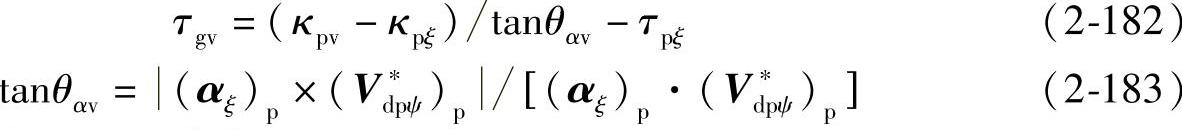
（3）Σ_p沿α_η方向的法曲率和短程挠率

由式（2-39）和式（2-40），可得到Σ_p沿α_η方向的法曲率为

κ_pη=κ_pv-（τ_gv-τ_pξ）/tanθ_αv （2-184）

短程挠率为

τ_pη=-τ_pξ （2-185）