刀刃双自由度运动的分解方法探讨

1.刀盘、产形轮和轮坯的位置

以直线刀刃端铣刀盘D，用连续分度法加工摆线齿锥齿轮和准双曲面齿轮i时，在刀盘与轮坯之间，有一个隐形产形轮P（简称产形轮），与铣齿机的摇台共轴线，但两者不是一体^[14]。加工右旋齿轮时，刀盘D、产形轮P和轮坯i的位置如图2-4所示。

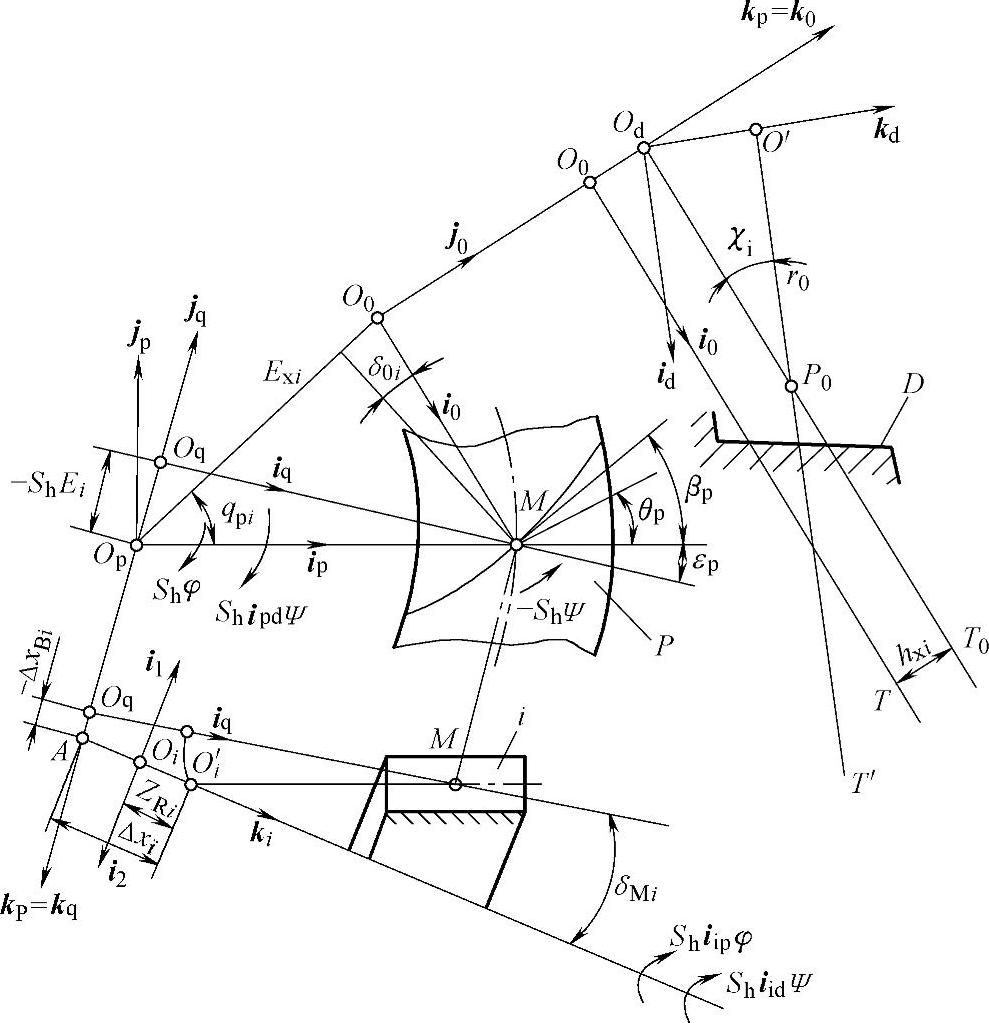
图2-4 刀盘、产形轮和轮坯的位置

取右旋直角坐标系σ_d（O_d；i_d，j_d，k_d）与摇台固连，k_d与刀盘轴线重合；σ_p（O_p；i_p，j_p，k_p）与机架固连，k_p与产形轮轴线（摇台轴线）重合；σ_i（O_i；i_i，j_i，k_i）与机架固连，加工小轮时i=1，加工大轮时i=2，O_i为被加工齿轮与相配齿轮轴线公垂线垂足（对于准双曲面齿轮），或两轴线交点（对于锥齿轮）^[14]，k_i=k₁=k₂与轮坯轴线重合，i₂=-i₁。取辅助坐标系σ₀（O₀；i₀，j₀，k₀）和σ_q（O_q；i_q，j_q，k_q）；j₀=j_d，k₀=k_p=k_q。

图2-4中M为齿面的参考点；P₀为刀齿节点；A为机床中心。过刀齿节点P₀垂直于刀盘轴线的平面T′为度量刀齿半径和刀齿高的基准面；T为未修正分锥角时，产形轮的分度平面是确定轮坯与铣齿机相对位置的基准面。T₀为基本齿廓中线所在平面。

利用回转矩阵法进行坐标变换^[10]，由图2-4得到各坐标系的变换矩阵如下：

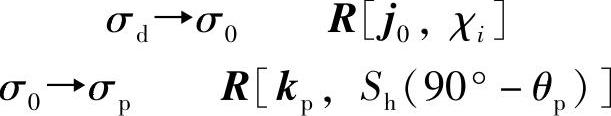
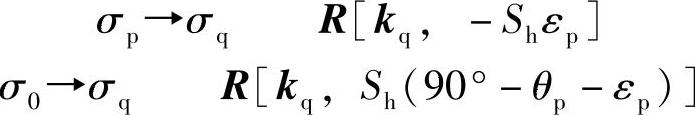
加工齿轮1时

σ_q→σ₁ [M_q1]=R[j₁，-（90°-δ_M1）]

加工齿轮2时

σ_q→σ₂ [M_q2]=R[j₂，90°-δ_M2]R[k₂，180°]

在变换矩阵中各参数为

θ_p=β_p-δ_0i

式中 β_p——产形轮参考点M的螺旋角；

δ_0i——T₀面上刀齿方向角。

ε_p=arcsin[sin（β_mi-β_p）cosδ_i/sinΣ_pi]

式中 ε_p——产形轮偏离角^[14]；

β_mi——被加工齿轮参考点M的螺旋角；

δ_i——被加工齿轮分锥角；

Σ_pi——产形轮P与被加工齿轮i的轴交角；

χ_i——刀倾角；

δ_Mi——轮坯安装角。(www.xing528.com)

2.刀盘、产形轮和轮坯的相对运动

刀盘D有z₀组刀齿，每组至少有两个刀齿，即加工齿凹面的外刀A和加工齿凸面的内刀I。为实现连续分度，刀盘每转过一组刀齿，齿数为z_p的产形轮P和齿数为z_i的轮坯i各转过一个齿。轮坯与刀盘的传动比i_id=z₀/z_i，产形轮与刀盘的传动比i_pd=z₀/z_p；轮坯与产形轮的传动比i_ip=z_p/z_i。连续分度运动参数为刀盘转角ψ。产形轮P展成轮坯i的运动参数为产形轮转角φ。

考虑到加工左旋和右旋齿轮刀盘旋转方向不同，以及刀位角符号不同等因素，在下文的通用公式中引入符号系数S_h：加工左旋齿轮S_h=1，加工右旋齿轮S_h=-1。

刀盘D转角ψ_d=-S_hψ

产形轮P总转角φ_p=S_h（i_pdψ+φ）

轮坯i总转角φ_i=S_h（i_idψ+i_ipφ）

刀盘角速度矢量

产形轮角速度矢量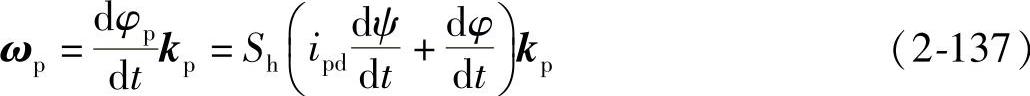

轮坯角速度矢量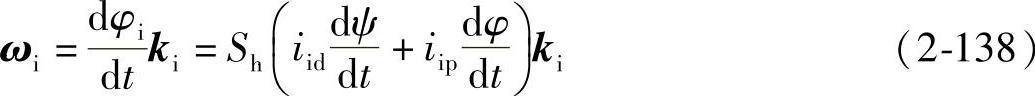

转角ψ和φ的正向，分别由回转轴线的单位矢量k_d、k_p和k_i按右手定则确定，即大拇指指向与各单位矢量相同时，其余四指的旋向为转角正向。

刀盘D与轮坯i的相对角速度为

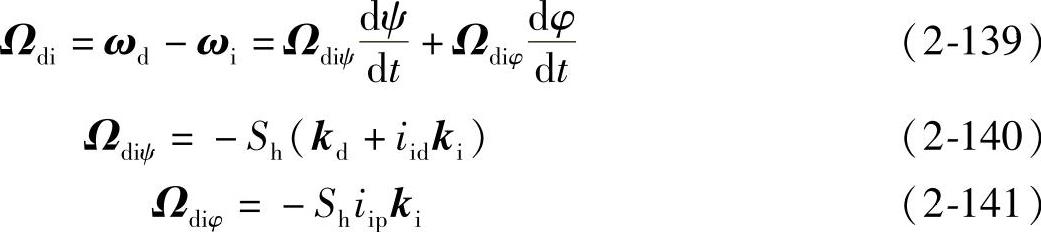
刀盘D与产形轮P的相对角速度为

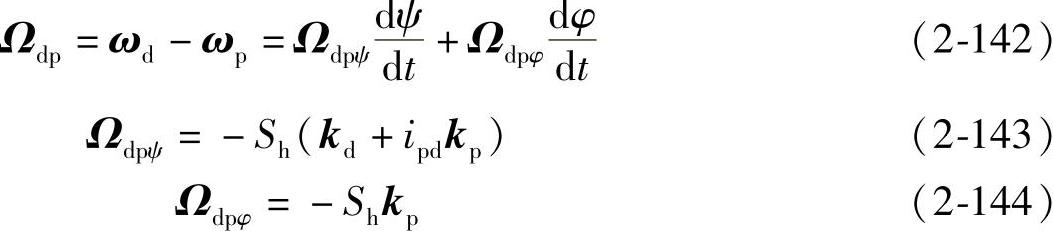
产形轮P与轮坯i的相对角速度为

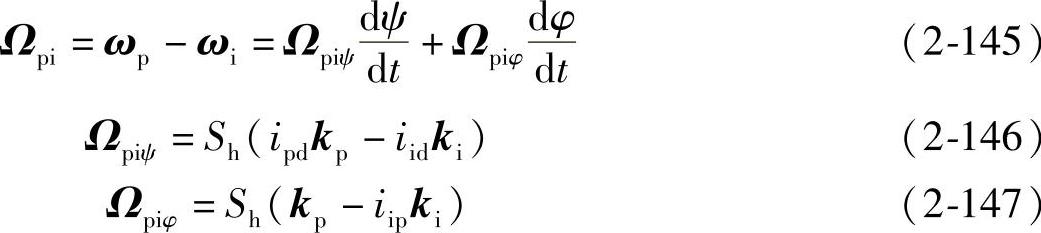
转角ψ和φ是两个独立的运动参数：ψ保证连续分度铣齿，由切削速度确定刀盘的角速度ω_d；φ完成展成铣齿运动，由进给量确定产形轮关于φ的角速度ω_pφ。

3.双自由度运动的分解

铣齿面Σ_i时，直线刀刃Γ_d的双自由度运动是同时进行的，为了简化计算，可分别按运动参数ψ和φ将其分解如下：

1）直线刀刃Γ_d按关于ψ的相对角速度Ω_diψ运动，在轮坯i上形成轨迹曲面Σ′_i，此面为无展成运动开槽形成的齿面。

2）直线刀刃Γ_d按关于ψ的相对角速度Ω_dpψ运动，在产形轮P上形成轨迹曲面Σ_p，此面为产形轮P的虚拟产形面（下文简称产形面）。

3）产形轮P的产形面Σ_p，按关于φ的相对角速度Ω_piφ运动，展成齿轮i，将轨迹曲面Σ′_i展成齿面Σ_i。