蜗杆螺旋面的方程与曲率参数

（1）在σ_0e里曲面族{Σ_d}_0e的方程

当蜗杆转过φ角时，σ_e绕k_0e转过（i_d1φ）角。Σ_d在σ_0e里形成曲面族{Σ_d}_0e，将式（2-83）进行σ_e→σ_0e坐标变换，得到{Σ_d}_0e的方程为

（r_e）_oe=r_be_oe（θ+φ_d）-r_bθg_oe（θ+φ_d）+p_dμk_d （2-113）

将式（2-94）、式（2-95）和式（2-93）进行σ_e→σ_0e坐标变换，在σ_0e里，Σ_d上活动标架的单位矢量为

（α_dξ）_0e=e_0e（θ+φ_d） （2-114）

（α_dη）_0e=sinβ_bg_0e（θ+φ_d）+cosβ_bk_0e （2-115）

（n_d）_0e=sinβ_bk_0e-cosβ_bg_0e（θ+φ_d） （2-116）

（2）σ_e与σ₁的相对角速度和相对速度

由式（2-73）得相对角速度为

（ω_e1）_0e=（Ω_d1φ）_0e=i_d1k_0e-j_0e （2-117）

由式（2-79）得相对速度为

（v_e1）_0e=（V_d1φ）_0e=（i_d1k_0e-j_0e）×（r_d）_0e+a_dk_0e-si_0e （2-118）

（3）Σ_d与Σ₁的共轭条件函数

将式（2-113）和式（2-116）代入式（2-45）得

（R）_0e=（p_dμcosβ_b-r_bθsinβ_b）e_0e（θ+φ_d）-r_bsinβ_bg_0e（θ+φ_d）-r_bcosβ_bk_0e （2-119）

将式（2-120）～式（2-122）代入式（2-46）得

（v₀）_0e=-a_dk_0e+si_0e （2-123）

将式（2-116）、式（2-117）、式（2-119）和式（2-123）代入式（2-44），得Σ_d和Σ₁的共轭条件函数为

为便于求解，令

ψ=θ+μ （2-125）

由共轭条件方程Φ_d=0得

给定φ值，给出ψ值，由式（2-126）求得θ值，由式（2-125）求μ值。代入式（2-83），得到Σ_d上的一个接触点。改变ψ值则得到一条瞬时接触线。给出不同的φ值得到Σ_d上的瞬时接触线族。

（4）啮合界线函数

将式（2-124）对t求偏导数，并考虑到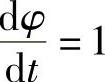，得

由式（2-83）和Φ_d=Φ_dt=0，得Σ_d上的啮合界线，令式（2-124）中Φ_d=0，并乘以cos（θ+φ_d）；令式（2-127）中Φ_dt=0，并乘以sin（θ+φ_d）；将两者相减，并由式（2-125）代入μ值后得

给出不同的φ值，由式（2-128）求得ψ，由式（2-126）求得θ，由式（2-125）求得μ，代入式（2-83），可以得到Σ_d上的啮合界线Φ_dt。(www.xing528.com)

由式（2-128）可知，Σ_d上啮合界线存在的范围为

-1≤cos（ψ+i_d1φ）≤1

cos（ψ+i_d1φ）≥-1时，由式（2-128）得

cos（ψ+i_d1φ）≤1时，由式（2-128）得

若所选β_b值为β_bA≥β_b≥β_bB，则Σ_d面上无啮合界线。

由啮合分析可知，取β_b=β_bA时，Σ_d上瞬时接触线分布最好。

分度圆螺旋角β可由下式求得：

sinβ=sinβ_b/cosα_n （2-131）

式中 α_n——渐开螺旋面Σ_d的分度圆法向压力角。

由式（2-91）和式（2-92）得Σ_d的螺旋参数为

p_d=r_b/tanβ_b （2-132）

（5）环面蜗杆螺旋面的方程

由式（2-48）和式（2-113）进行σ_0e→σ₁坐标变换，得曲面族{Σ_d}₁在σ₁里的方程为

由式（2-133）和式（2-126）可以得到环面蜗杆螺旋面Σ₁的方程。

（6）曲率干涉界线函数

由κ_dη=0和τ_dξ=0，式（2-51）和式（2-52）可写成

由式（2-50）求得（N_d）_0e，由式（2-49）求得Ψ_d。由式（2-133）、式（2-126）和Ψ_d=0，求得蜗杆螺旋面上的曲率干涉界线。

（7）蜗杆螺旋面Σ₁的曲率参数

由式（2-53）～式（2-55），可求得Σ_d与Σ₁沿α_dξ和α_dη方向的诱导法曲率κ_d1ξ和κ_d1η以及诱导短程挠率τ_d1ξ。

由式（2-56）～式（2-58），可求得蜗杆螺旋面沿α_1ξ=α_dξ和α_1η=α_dη方向的法曲率κ_1ξ、κ_1η以及沿α_1ξ方向的短程挠率τ_1ξ。

（8）Σ_d与Σ₁接触点的滑动角

v_e1方向与瞬时接触线方向的夹角θ_vt为滑动角，可由式（2-59）求得。

（9）环面蜗杆渐开线齿轮副

由渐开线双自由度运动展成的环面蜗杆1，可以与渐开线齿轮2组成环面蜗杆渐开线齿轮副，条件是：传动比i₂₁=i_d1；中心距a=a_d；齿轮的基圆半径r_b2=r_b；p_d2=p_d（或β_b2=β_b）；即齿轮2的齿面与Σ_d相同。

这种传动的特点是，蜗轮就是一个普通的渐开线斜齿圆柱齿轮，可以加工到很高的精度。环面蜗杆可以用渐开线齿轮珩磨，可以提高其加工精度和降低齿面粗糙度。