轨迹曲面Σd的方程和曲率参数解析

（1）轨迹曲面Σ_d的方程

σ_d按参数s相对于σ_e运动时，渐开线Γ_d形成轨迹曲面Σ_d，其方程为

（r_e）_e=（r_d）_e+sk_e （2-81）

将式（2-61）进行σ_d→σ_e坐标变换得

（r_d）_e=r_be_e（θ+μ）-r_bθg_e（θ+μ） （2-82）

将式（2-82）和s=p_dμ代入式（2-81）得

（r_e）_e=r_be_e（θ+μ）-r_bθg_e（θ+μ）+p_dμk_e （2-83）

以μ代换s之后，式中θ和μ为轨迹曲面Σ_d的参数。Σ_d为渐开线螺旋面。

（2）σ_d与σ_e的相对角速度和相对速度

相对角速度矢量为

相对速度矢量为

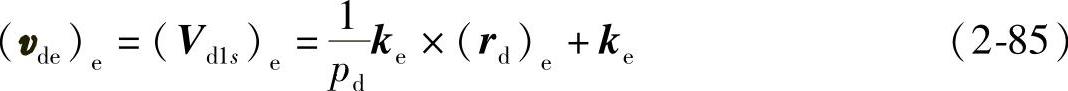
将式（2-82）代入式（2-85）得

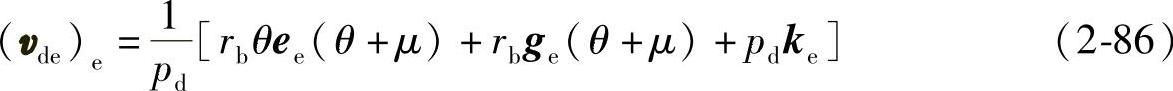
（3）轨迹曲面上的活动标架

将式（2-65）、式（2-68）和式（2-67）进行σ_d→σ_e坐标变换得

（α）_e=e_e（θ+μ） （2-87）

（β）_e=g_e（θ+μ） （2-88）

（γ）_e=k_e （2-89）

将式（2-86）和式（2-87）代入式（2-16）得轨迹曲面Σ_d的单位法矢量为

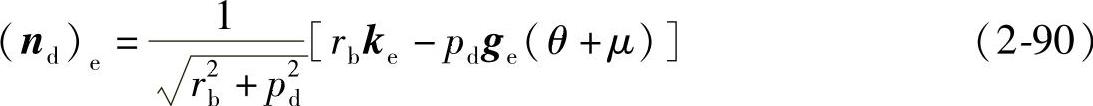
若渐开螺旋面的基圆螺旋角为β_b，则

将式（2-91）和式（2-92）代入式（2-90）得

（n_d）_e=sinβ_bk_e-cosβ_bg_e（θ+μ） （2-93）

在Σ_d上任一点M处建立活动标架（M；α_dξ，α_dη，n_d），取

（α_dξ）_e=（α）_e=e_e（θ+μ） （2-94）

（α_dη）_e=（n_d）_e×（α_dξ）_e=sinβ_bg_e（θ+μ）+cosβ_bk_e （2-95）

（4）轨迹曲面Σ_d的曲率参数

由式（2-34）得Σ_d沿α_dξ=α方向的法曲率为

κ_dξ=κ_nα=κ（β）_e（n_d）_e

将式（2-88）和式（2-93）代入上式得

κ_dξ=κ_nα=-κcosβ_b （2-96）

式中 κ——曲线Γ_d的曲率，由式（2-69）求得。

由式（2-35）得Σ_d沿α_dξ方向的短程挠率为(https://www.xing528.com)

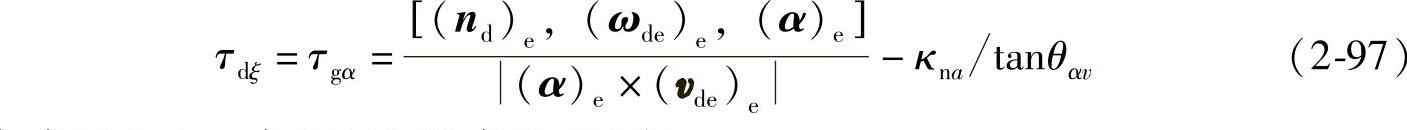
由式（2-84）、式（2-87）和式（2-93）得

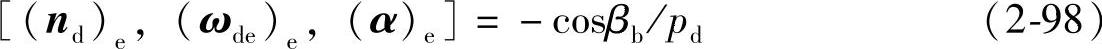
由式（2-86）和式（2-87）得

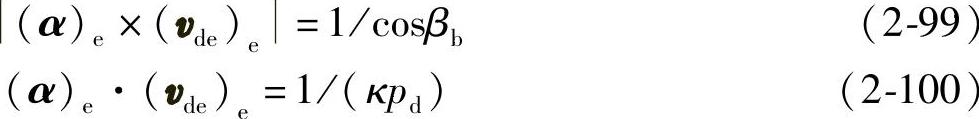
由式（2-36）计算由α_dξ至v_de的有向角θ_αv，即

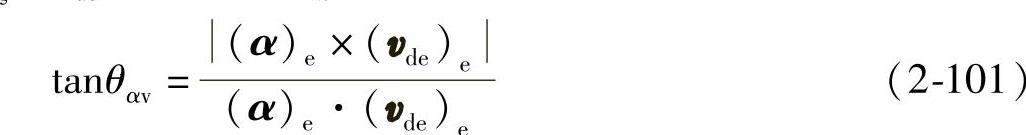
将式（2-99）和式（2-100）代入上式得

tanθ_αv=κp_d/cosβ_b （2-102）

将式（2-96）、式（2-98）、式（2-99）和式（2-102）代入式（2-97）得

τ_dξ=τ_gα=0

α_dξ方向是渐开螺旋面Σ_d的主方向，因而α_dη为Σ_d的另一主方向，其短程挠率为

τ_dη=-τ_dξ=0

由式（2-37）得Σ_d沿v_de方向的法曲率为

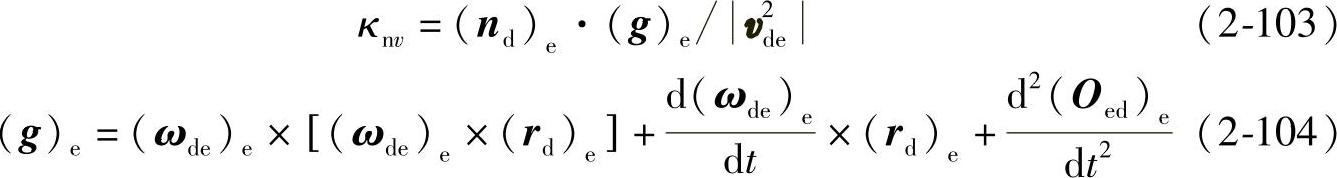
考虑到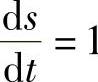，式（2-104）中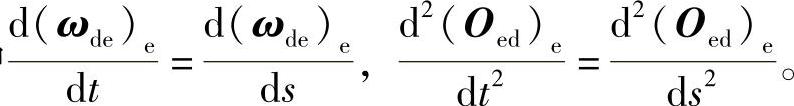

将式（2-84）对s求导，得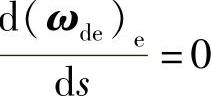。由图2-2得

（O_ed）_e=sk_e （2-105）

将式（2-105）对s求二阶导数，得

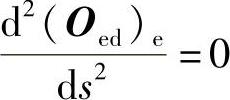
将式（2-84）代入式（2-104）得

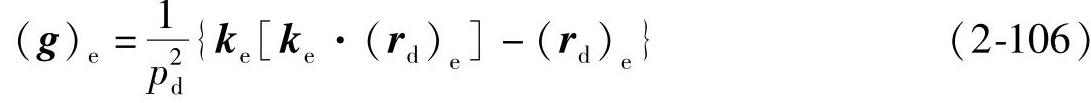
由式（2-86）得

（v_de）2=G/p²_d （2-107）

G=（r_bθ）2+r²_b+p²_d （2-108）

将式（2-93）、式（2-106）和式（2-107）代入式（2-103）得

κ_nv=-cosβ_b/（κG） （2-109）

将式τ_dξ=τ_gα=0代入式（2-38）得Σ_d沿v_de方向的短程挠率为

τ_gv=（κ_nv-κ_dξ）/tanθ_αv （2-110）

将式（2-96）、式（2-102）和式（2-109）代入式（2-110）得

τ_gv=p_d/G （2-111）

将τ_dξ=τ_gα=0代入式（2-39）得Σ_d在α_dη方向的法曲率为

κ_dη=κ_nv+τ_gv/tanθ_αv （2-112）

将式（2-102）、式（2-109）和式（2-111）代入式（2-112）得

κ_dη=0