【摘要】：于是将式代入式后得式乘以ds1得d1r1和δ1r1的方向不同，但它们都表示Σ1在点M1处的任一切矢量，式可改写成式除以δs2得将式代入式可得由式得到联立方程解联立方程得将式和式代入式，并考虑到式的关系，得到齿面Σ1和Σ2接触点处沿任一α方向的诱导法曲率为令由αξ方向到α方向的有向角为γ，则式中，Njξ和Njη由式和式求得。
设齿面Σ1的单位法矢量n1由齿轮1齿的实体指向空域，在齿面Σ1接触点M1处的切平面上任取一方向，其单位矢量为
式中，s1和s2为沿同一方向α齿面Σ1和Σ2的法截线Γ1和Γ2的弧长。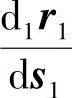
的共轭方向
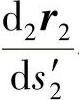与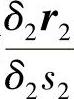
不同，因此用不同的符号表示导数。
沿α方向，齿面Σ1和Σ2的法曲率为
可以证明式（1-102）中
d1r1·δ1n1=d1n1·δ1r1[10] （1-103）
将式（1-103）代入式（1-102）得
将式（1-100）代入式（1-104），得到α方向的诱导法曲率为
将式（1-3）和式（1-6）代入式（1-105）得
式中，φj为运动参数，t为时间，对于齿面Σ1上点M1处不同的切线方向，它们都是相同的，即dφj=δφj，dt=δt。于是将式（1-85）代入式（1-106）后得
式（1-83）乘以ds1得(www.xing528.com)
d1r1和δ1r1的方向不同，但它们都表示Σ1在点M1处的任一切矢量，式（1-108）可改写成
式（1-109）除以δs2得
将式（1-66）代入式（1-110）可得
由式（1-111）得到联立方程
解联立方程得
将式（1-113）和式（1-114）代入式（1-107），并考虑到式（1-86）的关系，得到齿面Σ1和Σ2接触点处沿任一α方向的诱导法曲率为
令由αξ方向到α方向的有向角为γ，则
式中，Njξ和Njη（j=1，2）由式（1-79）和式（1-80）求得。将N1α和N2α代入式（1-115）得
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
