式(1-67a)为Nj的第一种计算公式。
将式(1-39)和式(1-40)代入式(1-67a)得

式(1-71)展开后得
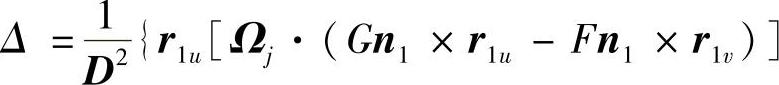
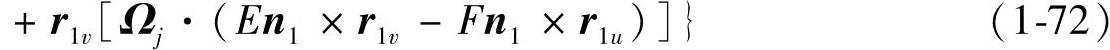
在式(1-72)中
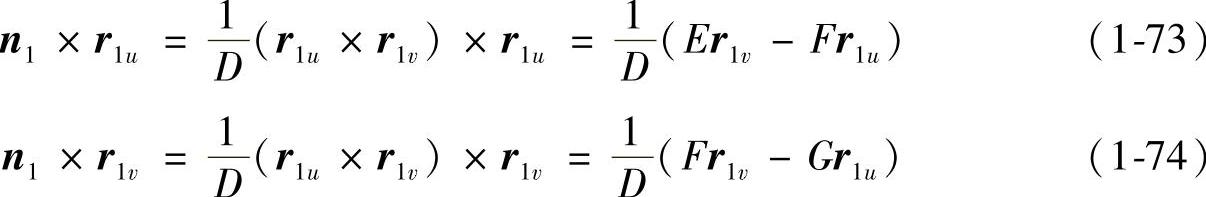
将式(1-73)和式(1-74)代入式(1-72),化简后得
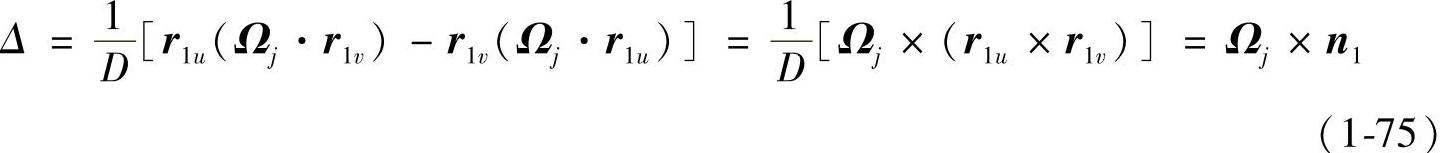
将式(1-75)代入式(1-70),得到Nj的第二种计算公式为
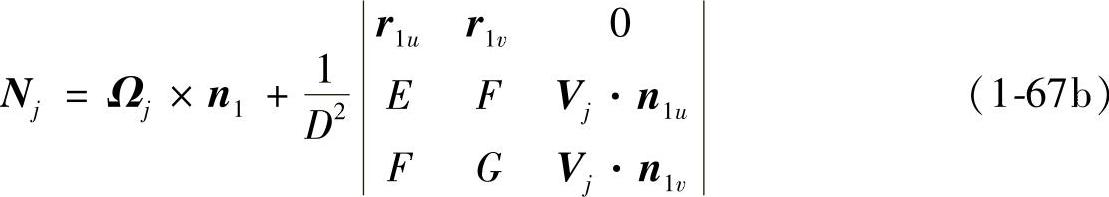
齿面Σ1上点M1处的主方向单位矢量分别为g1和g2,主曲率为κ1和κ2。取活动标架(M1;g1,g2,n1);以Σ1上的曲率线为参数曲线,可得到
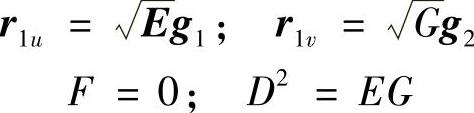
由微分几何中的Rodrigues方程可得到
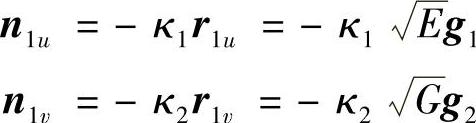
将上面各式代入式(1-67b)得
Nj=Ωj×n1+κ1(Vj·g1)g1+κ2(Vj·g2)g2 (1-76)
将
Ωj×n1=Ωj×(g1×g2)=g1(Ωj·g2)-g2(Ωj·g1)
代入式(1-76),得到Nj的第三种计算公式为
Nj=λg1+μg2 (1-67c)
λ=κ1(Vj·g1)+Ωj·g2 (1-77)(https://www.xing528.com)
μ=κ2(Vj·g2)-Ωj·g1 (1-78)
在齿面Σ1的点M1处的切平面上,任取互相垂直的两方向αξ和αη,由主方向g1至αξ的有向角为φξ(见图1-3)。取活动标架(M1;αξ,αη,n1),可得到
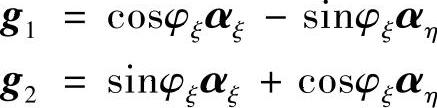
上两式分别对Ωj和Vj取数积,得
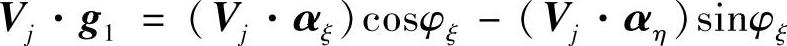
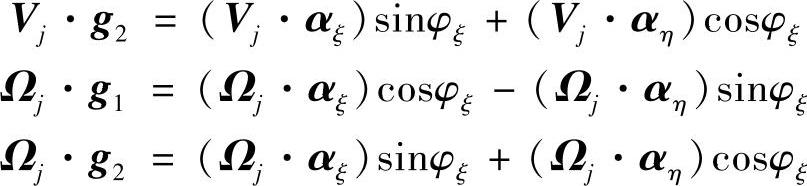
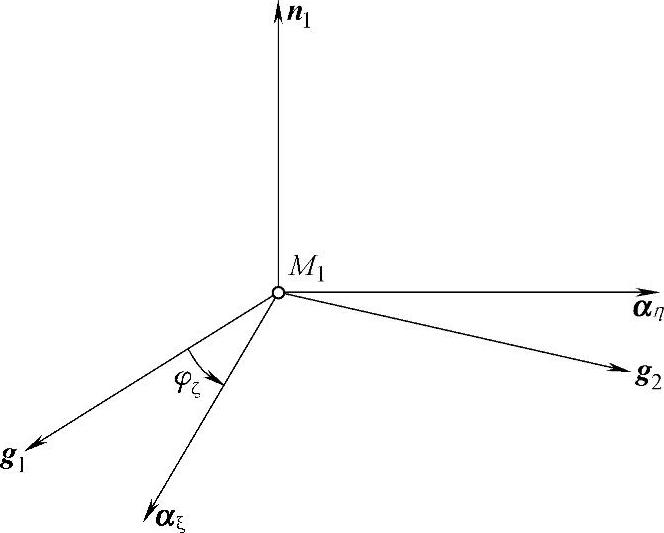
图1-3 活动标架(M1;αξ,αη,n1)
将以上六式代入式(1-67c),并利用Euler公式和Bertrand公式加以简化,得到Nj的第四种计算公式为
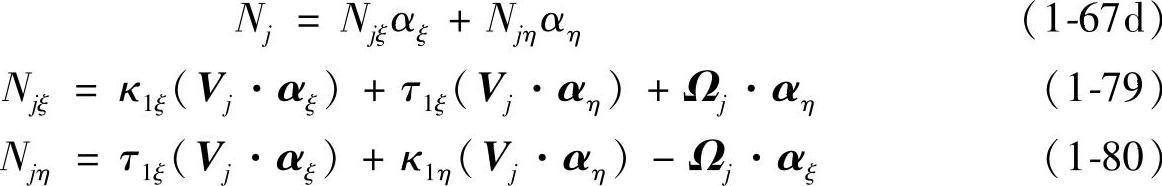
式中 κ1ξ、κ1η——齿面Σ1在点M1处沿αξ和αη方向的法曲率;
τ1ξ——齿面Σ1在点M1处沿αξ方向的短程挠率。
取αξ=αα=Vj/Vj,αη=αβ=n1×Vj/Vj,κ1ξ=κ1Vj和τ1ξ=τ1Vj。将各参数代入式(1-67d)、式(1-79)和式(1-80)后,得到Nj的第五种计算公式为
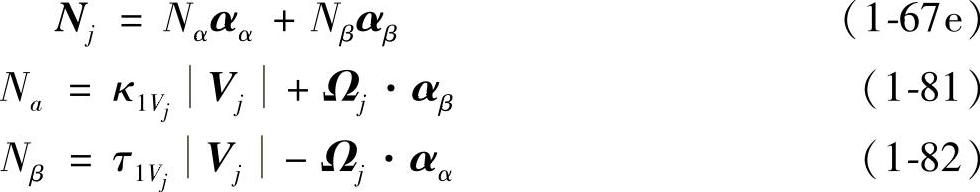
将式(1-81)和式(1-82)代入式(1-67e),得到Nj的第六种计算公式为
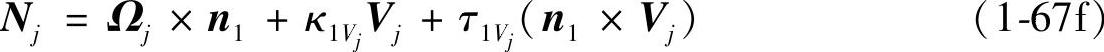
将式(1-67f)代入式(1-46)得
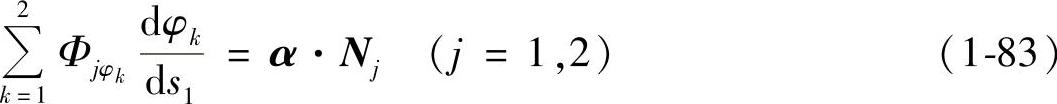
将式(1-41)代入式(1-34)得
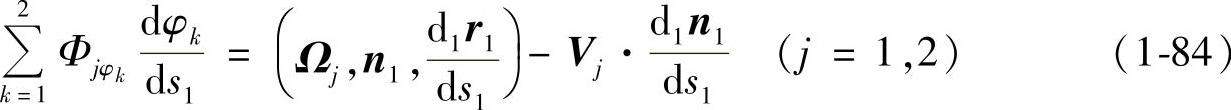
由式(1-83)和式(1-84)得
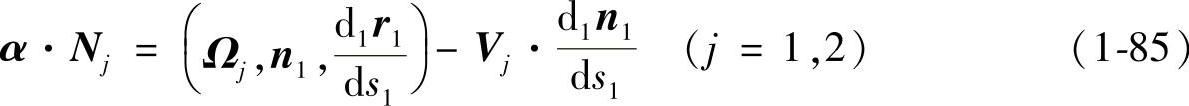
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




