【摘要】：双自由度啮合（n=2）时，对于给定的一组值，如果由式求得u=；v= 则齿面Σ1上得到1个接触点。曲线φ1和φ2在Σ1上形成新的网络。为求偏导数，将式代入式，并对φk求偏导数，得φ1和φ2为独立参数，，由式得解上面方程组得式中将式代入式和式得由式得当 时，在齿面Σ1上得到r1φ1×r1φ2=0的特征点。将式代入式得通常，齿面Σ1上特征点的条件为按特征点的条件Φt=0，存在三种情况：
双自由度啮合（n=2）时，对于给定的一组（φ1，φ2）值，如果由式（1-12）求得
u=（φ1，φ2）；v=（φ1，φ2） （1-47）
则齿面Σ1上得到1个接触点。当φ2为常数时，改变φ1在Σ1上得到曲线φ1；φ1为常数时，改变φ2在Σ1上得到曲线φ2。曲线φ1和φ2在Σ1上形成新的网络。将式（1-47）代入式（1-1），用参数φ1和φ2代换u和v，得
r1=r1[u（φ1，φ2），v（φ1，φ2）]=r1（φ1，φ2） （1-48）
对式（1-48）取关于坐标系σ1的相对微分，有
d1r1=r1φd1φ1+r1φd2φ2 （1-49）
式中 
微分几何中已经证明，参数代换必须满足雅可比行列式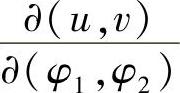
≠0。
为求偏导数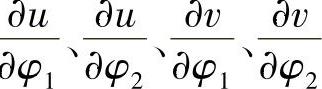
，将式（1-47）代入式（1-11）（令n=2），并对φk求偏导数，得
φ1和φ2为独立参数，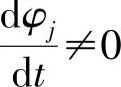
，由式（1-52）得(www.xing528.com)
解上面方程组得
式中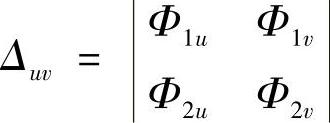 
将式（1-54）代入式（1-50）和式（1-51）得
由式（1-49）得
当 
时，在齿面Σ1上得到r1φ1×r1φ2=0的特征点。
将式（1-54）代入式（1-57）得
通常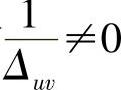
，齿面Σ1上特征点的条件为
按特征点的条件Φt=0，存在三种情况：
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
