以某一轴向应变值 (一般取5%)为破坏标准作振动三轴试验,用Mohr圆求出破坏面上的固结剪应力τcf和动剪应力τdf,如图4.20 (单向振动)或图4.22 (双向振动)所示。按坝址处的设计等效振动次数,整理出τf~αc~σcf关系曲线,如图7.27 所示,其中τf=τcf+τdf,σcf为破坏面上的固结正应力,αc为固结剪应力比τcf/σcf。
根据非线性有限元计算得到的坝体静应力成果,利用图7.28 中Mohr 圆将滑弧通过的各单元的静应力σy、σz、τxy转换为滑弧切线上的正应力σs和剪应力τs,即
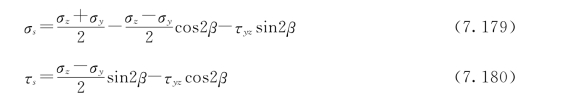
式中 β——通过该单元的滑弧切线与水平线的夹角。
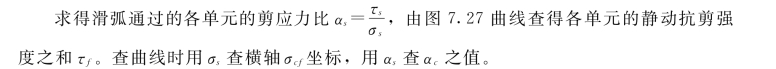
同样,根据动力非线性有限元计算得到的坝体动应力成果,将滑弧通过的各单元的动应力σy,d、σz,d、τxy,d用图7.28 中方法换算成滑弧切线上的动正应力σd和动剪应力τd,则滑弧切线上的静动剪应力之和为τ=τs+τd。
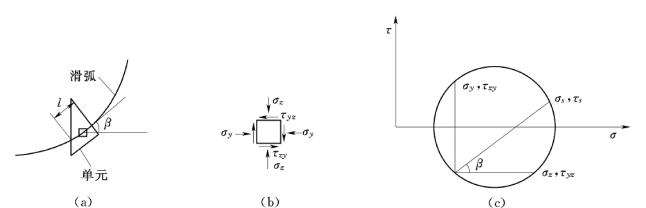
图7.28 单元内滑弧切线上正应力和剪应力计算
滑弧通过的第i 单元的长度为li,该单元的静动抗剪强度之和为τfi,静动剪应力之和为τi,则整个滑弧的抗滑安全系数K 为(https://www.xing528.com)

具体计算步骤如下:
(1)假定滑弧圆心和半径。
(2)寻找滑弧穿过的单元,求得滑弧穿过的每个单元处的滑弧长度li和滑弧切线与水平线的夹角βi。
(3)进行非线性有限元静力计算和动力计算,将计算得到的滑弧穿过的每个单元的静应力和动应力转化到滑弧切线上。
(4)计算滑弧穿过的各个单元的抗剪力τfili及剪切力τili。
(5)利用式(7.181)求抗滑安全系数K。
(6)重复上述步骤,得到最小的K,即为所求的抗滑安全系数。
可以看出,上述抗滑安全系数K 是试样产生某一轴向应变时的抗剪强度对于坝体剪应力的安全度,并非坝坡失稳时的抗滑稳定安全系数,且动抗剪强度未与坝体的动应力反应发生联系,与前述总应力法验算液化的缺点相同。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




