坝体G为常数时的地震反应计算

1.自振频率和振型计算

由式（7.1）可得坝体自振方程为

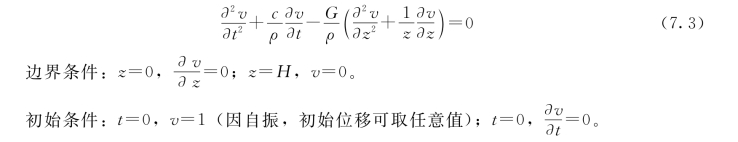
采用分离变量法，令v＝Φ（z）Y（t），此处Φ（z）为无量纲振型，Y（t）为广义坐标或正则坐标，即振型的时间函数，使式 （7.3）分为只有变量t 以及只有变量z 的两个微分方程[以下略去角标（z）、（t），也略去振型阶数n]

将式（7.7）和式（7.8）代入式（7.5），整理后得

式 （7.9）为零阶贝塞尔方程，其通解为

式中 J0——第一类零阶贝塞尔函数；

N0——第二类零阶贝塞尔函数。

将式（7.10）对z 求偏导，得

式中 J1——第一类一阶贝塞尔函数；

N1——第二类一阶贝塞尔函数。

由于振型Φ是无量纲相对值，故可取A1＝1。

再将边界条件z＝H，Φ＝0 代入式（7.12），得

第一类零阶贝塞尔函数有无数个零点（根），以β0，n代表这些根，前5 个根为

前5 阶振型的自振频率为

低坝或堤防的顶宽与底宽之比在0.1 以上时，顶部宽度对堤坝的自振特性有一定影响，应对按三角形剖面推导的自振频率和振型进行校正。自振频率可用下式校正

式中 B0——堤坝的顶宽；

B——堤坝的底宽。

不同B0/B 的土石坝断面，其振型可按三角形断面（B0/B＝0）的振型和矩形断面（B0/B＝1）的振型用内插法求取。三角形断面的振型见式（7.14），矩形断面的振型公式为：

几座土石坝的实测自振周期列于表7.1，供参考。

表7.1　几座土石坝实测自振周期

注 （）中数字为覆盖层厚度。

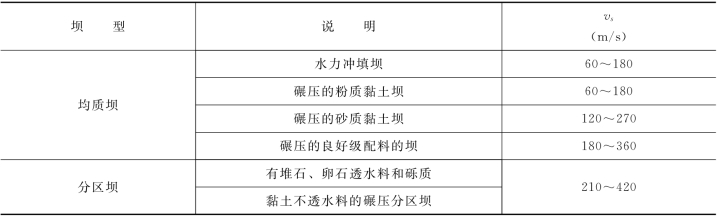
土石坝的剪切波速vs列于表7.2，供计算自振频率时参考。

表7.2　土石坝的剪切波速vs(www.xing528.com)

关于正则坐标Y（t）的求解，由于式 （7.6）与式 （2.2）形式相同，故其解与式（2.9）相同，即

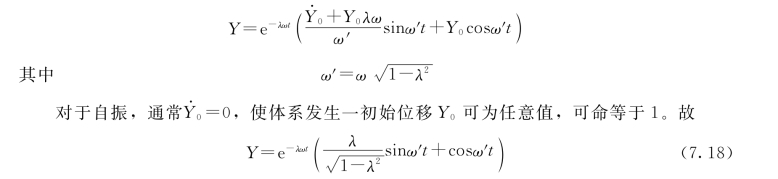
2.地震反应计算

式 （7.19）两端乘某阶振型的ρzΦ，利用不同阶振型关于质量和阻尼的正交特性 （即振型的正交性定理），则仅剩下与ρzΦ同阶振型的各物理量乘积，即

振型Φ的微分方程与式（7.5）相同，故振型Φ的解答同式（7.14），即

将振型Φ代入振型参与系数η中，积分后得

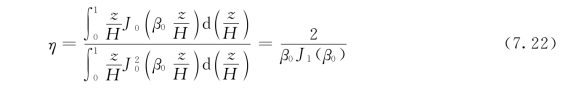
正则坐标Y 的微分方程式 （7.21）与式 （2.170）形式相同，对照其解 [式（2.171）]，可得

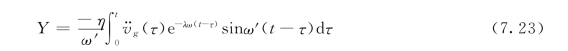
利用振型叠加法得到的位移反应如下

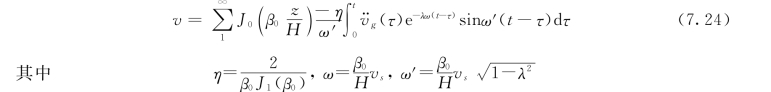
实际计算时，式 （7.24）只需取前3～4 项之和，即前3～4 阶振型和频率即可。杜哈姆积分按地震加速度时程曲线用数值积分法进行。

前4 个第一类零阶贝塞尔函数的根为

由附录二的表Ⅱ查取得

故前4 阶振型参与系数为

对位移反应关于时间t 求偏导得到速度反应，如下

对位移反应关于时间t 求二阶偏导得到加速度反应，如下

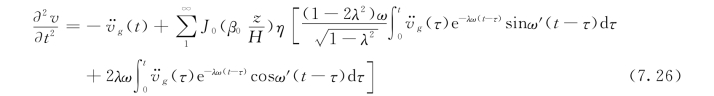
绝对加速度反应

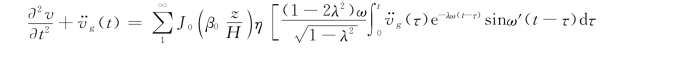
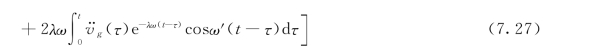
对位移反应关于z 求偏导得到剪应变反应，如下

剪应力反应

以上各式中，一般取有限项振型即可。