坝体与地基单元设计优化

坝体和地基单元的基本形式是8 结点六面体等参单元。为了适应边界的不规则形状，还采用6 结点三棱柱等参单元和4 结点四面体单元，如图6.1 所示。

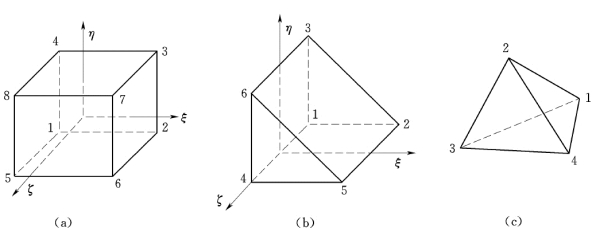
图6.1　坝体及地基单元

（a）六面体单元；（b）五面体单元；（c）四面体单元

1.单元位移模式及形函数

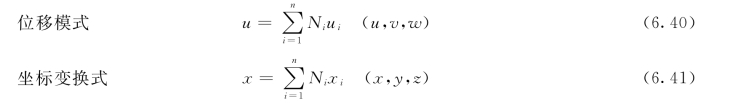
式中 Ni——单元的形函数；

n——单元的节点数，如8、6、4 等。

8 结点六面体等参单元的形函数为

6 结点三棱柱等参单元的形函数为

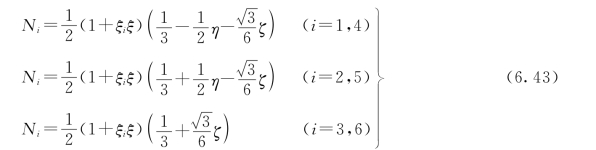
4 结点四面体单元的形函数为

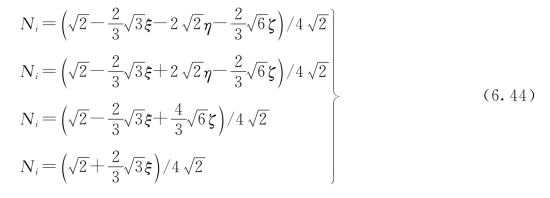
2.单元应变表达式

单元的应变

将位移模式（6.40）代入式（6.45），得

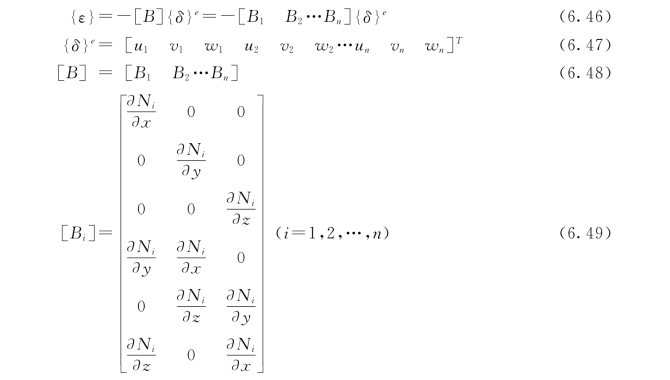
式中 n——单元结点数；

｛δ｝e——单元结点位移列阵；

[B]——应变转换矩阵，即(www.xing528.com)

弹性条件下单元的应力

式中 [D ]——弹性矩阵，可用拉梅常数λ和G 表示，见式（6.6）。

3.等参单元Jacobi 矩阵和高斯积分

在求单元应力和应变时，必须求出式 （6.48）应变转换矩阵 [B]的每一个元素，它们是形函数对整体坐标的偏导数。为此，应先求出形函数对局部坐标的偏导数

式中 r、s、t——ξ、η、ζ方向的高斯积分点数；

ξi、ηj、ζk——ξ、η、ζ方向高斯积分点的局部坐标；

Hi、Hj、Hk——相应积分点的加权系数。

4.等参单元的劲度矩阵

由虚功原理可得

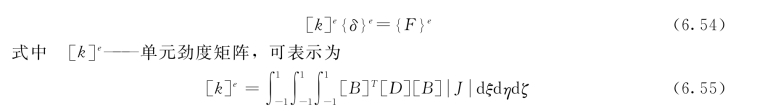
将式（6.48）、式 （6.6）和式 （6.52）代入式 （6.55），可得单元劲度矩阵具体表达式，写成分块矩阵的形式，即

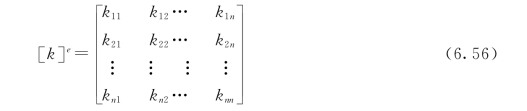
其中子矩阵为

式中 i，j——单元结点号，i＝1，2，…，n；j ＝1，2，…，n。

图6.2　接触面单元和止水连接单元

（a）六面体接触面单元；（b）五面体接触面单元；（c）六面体止水连接单元