Taniguchi等效惯性力法的优化策略

动应力与残余应变关系采用Taniguchi 等给出的一种在初应力条件q0/p′0下残余剪应变γr（本节中γr不是参考剪应变）与动、静应力幅值之间的关系曲线，如图5.18 所示。根据关系曲线有如下经验公式

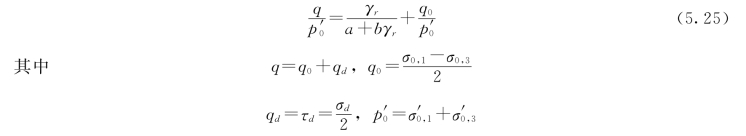
式中 σ′0，1、σ′0，3——初始大、小主应力；

σd——动应力幅值；

a、b——由试验确定的参数。

将式（5.25）的两边同时去掉静应力比项q0/p′0，则剩下动应力与残余应变关系，即

由于图5.18 中的试验曲线是相应于某一固结应力比Kc＝σ′0，1/σ′0，3和循环振动次数N下取得的，因此参数a、b 随固结应力比Kc和动应力循环振动次数N 而变。一般地，土石坝的固结应力比Kc变化范围多在1.5～2.5，地震荷载的等效循环振动次数Neq多在5～20。因此可以作出不同Kc和Neq下的关系曲线，由曲线拟合求得或曲线间插值求得相应的参数a、b 值。

(https://www.xing528.com)

（1）根据不同固结应力比Kc和循环振动次数N 下的试验曲线，输入相应的永久变形计算参数a （Kc，N）和b （Kc，N）。

（2）计算等效结点力。根据动力计算结果，将某一时段内均匀等效剪应力¯τ化为等效结点力，计算总的等效结点力。

（3）计算各单元的永久变形参数a 和b。由静力计算结果可求出各单元的固结应力比Kc，由动力计算结果可求出各单元在某时段的等效振动次数Neq。再由步骤（1）得到的a （Kc，N）和b （Kc，N）经插值求得各单元在t 时刻的动应力与残余应变关系曲线参数a 和b。

（4）静力计算结束时各单元的剪切模量G 作为初始剪切模量G0，形成劲度矩阵，作第一次迭代，并求出剪应变力γ1。

（5）由γ1，并通过步骤（3）求得的动应力与残余应变关系曲线，求出新的剪切模量G。与前一次的剪切模量G0比较，如不满足迭代控制条件，则继续迭代，求出新的位移、应变、应力和剪切模量G，直到满足迭代控制条件为止。满足迭代控制条件计算得到的变形就是永久变形。

刘汉龙的建议吸收了Serff等效结点力法中等效结点力的概念，克服了其动主应力差推求的不合理性。同时又吸收了Taniguchi等效惯性力法中直接采用由试验得到的动应力与残余应变关系曲线这一合理做法，且克服了该法中由结点加速度推求等效结点力时方向不易确定的缺点。