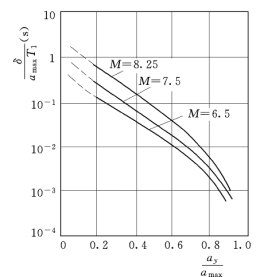
图5.6  关系曲线
关系曲线
Newmark法中滑动体为刚塑性体的假定与实际情况不符,计算结果的合理性和准确性值得商榷。1978 年,Makdisi和Seed在Newmark法的基础上进行了改进,提出采用将整个土石坝作为弹性体的解耦方法估算坝坡的地震滑移量。采用黏弹性本构模型对大坝进行地震动力反应非线性分析,确定潜在滑动体的平均地震加速度反应过程。再根据土料的抗剪强度,采用极限平衡分析法确定潜在滑动体的屈服加速度。最后将潜在滑动体平均地震加速度反应与屈服地震加速度相比较,确定地震过程中坝坡的超载历时,利用Newmark法估算潜在滑动体的滑移量。该法考虑了土体的非线性动力特性,克服了滑动体为刚塑性体假定的缺陷,具有一定的合理性。Martin、Seed、Ambrasseys、Sarma 等计算了几座坝高30~180m 的土石坝受到Elcentro 地震等8 次强烈地震的加速度反应,由这些反应曲线求得大坝各高程的最大平均加速度,即平均加速度时程曲线上的最大加速度峰值,用Newmark法计算了屈服加速度及水平向永久变形。Makdisi和Seed将其整理成正则化成果,得到不同震级 关系曲线,如图5.6 所示。其中δ为顺河向水平永久变形;T1为大坝的第一自振周期,表征坝高对水平向永久变形的影响;amax为滑动体部位的最大平均加速度;ay为滑动体的屈服加速度。图5.6 中的计算成果假定坝体的剪切波速为90~300m/s,剪切模量为常数,阻尼比采用0.2。计算得到的大坝第一自振周期为0.25~5s。
关系曲线,如图5.6 所示。其中δ为顺河向水平永久变形;T1为大坝的第一自振周期,表征坝高对水平向永久变形的影响;amax为滑动体部位的最大平均加速度;ay为滑动体的屈服加速度。图5.6 中的计算成果假定坝体的剪切波速为90~300m/s,剪切模量为常数,阻尼比采用0.2。计算得到的大坝第一自振周期为0.25~5s。
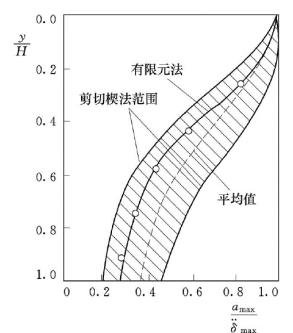
图5.7 amax/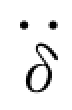 max与深度的关系
max与深度的关系
滑动体的最大平均加速度amax与坝顶最大加速度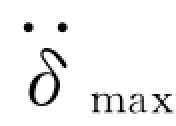 之比是从坝顶到坝基逐渐减小的。曾用Taft 地震波对一座坝高46m 的坝进行有限元分析,同时也用Elcentro地震波对许多假想坝用一维剪切楔法进行计算,并结合以往的研究成果,得到amax/δ··max在大坝中的分布规律,如图5.7 所示。由于所设计或研究的土石坝的剪切模量、阻尼比、剪切波速与图5.7中曲线计算时所采用的数据不同,受到的地震特性亦与Elcentro等8 次地震不同,土的屈服强度也不同,因此,在不做大坝的动力反应计算,直接用图5.7 估算得到的永久变形可能会有较大的误差。计算表明,当采用上限值时,其计算误差可能超过平均值的10%~30%。
之比是从坝顶到坝基逐渐减小的。曾用Taft 地震波对一座坝高46m 的坝进行有限元分析,同时也用Elcentro地震波对许多假想坝用一维剪切楔法进行计算,并结合以往的研究成果,得到amax/δ··max在大坝中的分布规律,如图5.7 所示。由于所设计或研究的土石坝的剪切模量、阻尼比、剪切波速与图5.7中曲线计算时所采用的数据不同,受到的地震特性亦与Elcentro等8 次地震不同,土的屈服强度也不同,因此,在不做大坝的动力反应计算,直接用图5.7 估算得到的永久变形可能会有较大的误差。计算表明,当采用上限值时,其计算误差可能超过平均值的10%~30%。
Makdisi Seed简化法的主要计算步骤如下:
(1)确定坝体土石料的抗剪强度参数c 和Φ。
(2)确定坝顶最大加速度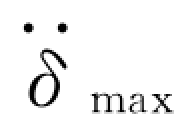 和大坝的第一自振周期T1=2π/ω1。
和大坝的第一自振周期T1=2π/ω1。
(3)选择可能滑动体在坝体中的位置,利用图5.7 确定滑动体的最大平均加速度amax。(https://www.xing528.com)
(4)对滑动体进行抗滑稳定计算,得到安全系数K 与水平向地震加速度aH的关系曲线,从而确定屈服加速度ay。

采用拟静力法对圆弧滑动体进行抗滑稳定计算,得到加速度aH与滑动稳定安全系数K的关系曲线,如图5.8 (b)所示。由该图查得安全系数K=1 时的屈服加速度ay。按平均强度指标①,查得屈服加速度ay=0.14g。按最小强度指标②,查得屈服加速度ay=0.07g。
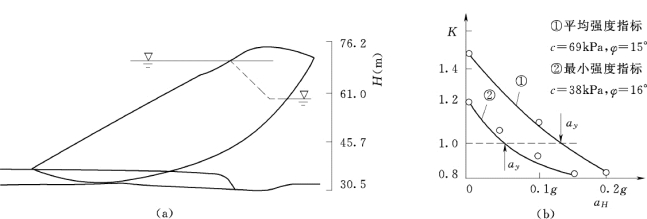
图5.8 永久变形的计算实例
(a)大坝滑动体示意图;(b)安全系数与屈服加速度的关系
按平均强度指标①,计算屈服加速度与最大加速度之比为

假设滑动体仅在上半坝高,即y/H=0.5,对平均强度指标①和最小强度指标②重复上述计算,则永久变形δ分别为0.06m和0.32m。这说明局部位移小于整体位移,整体滑动的永久变形是可能产生的最严重情况。上述计算结果与1906 年地震后实际观测情况基本相符。由于此计算工作是1977 年做的,验算1906 年Chabot坝的地震永久变形,难免有凑合之嫌。但作为分析,推算Chabot坝的填土强度为c=38kPa,Φ=16°,则有一定的可信度。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




