使用Newmark法进行结构动力学分析

1965 年，Newmark假定土坝为刚塑性体率先提出了地震永久变形计算方法。1978年，Makdisi和Seed以Newmark法为基础考虑土的弹塑性提出了简化计算方法。这个方法假定土坝受水平向地震作用时圆弧面滑动体朝水平方向移动，如图5.1 所示。土料在屈服应力以下发生弹性变形，地震时不会产生永久变形。土料超过屈服应力时，发生塑性变形，成为永久变形。

此法可用于计算碾压密实的黏性土坝、砂卵石坝和堆石坝的地震永久变形。

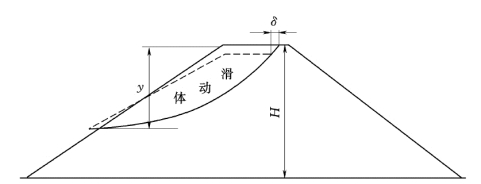
图5.1　滑动体

1.屈服加速度的确定

在确定屈服加速度之前，首先应确定土料在循环荷载振动下的屈服强度。对紧密黏性土和砂卵石，当循环荷载的动应力幅值较小时，即使循环次数很多，仅产生弹性变形。如图5.2 （a）所示，当循环应力 （静动力之和）约为静态不排水强度的80%时，循环100次几乎不产生永久变形。但是当循环应力达到静态不排水强度的95%时，循环10 次就产生较大的永久变形，如图5.2 （b）所示。Seed 等人对几种黏土原状样和重塑样进行了试验，以一定应变幅值施加200 次循环，然后作静力试验直到破坏，得到振动屈服强度与循环应变峰值曲线关系，如图5.3 所示。采用剪切楔法或有限元法等计算得到坝体各部位的动应变，求得滑动体的平均动应变后，与静态试验的破坏应变之比查图5.3，即可求得屈服强度。在无试验资料的情况下，碾压密实的黏性土和砂卵石的振动屈服强度可采用静态不排水强度的80%～90%。

图5.2　屈服强度

（a）80%不排水强度；（b）95%不排水强度

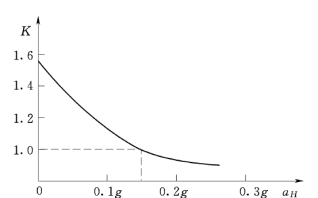
其次，对可能最危险的滑弧施加不同大小的水平向地震加速度aH，用拟静力法或动力法计算滑动体的抗滑稳定安全系数K，得到安全系数K 与水平向地震加速度aH的关系曲线，如图5.4 所示。其中，抗剪强度指标采用振动屈服强度。当抗滑稳定安全系数K＝1，滑动体达到极限平衡，与之对应的水平向地震加速度即为屈服加速度ay。屈服加速度与重力加速度的比值称为屈服地震系数，用KH，y表示。图5.4 中的屈服加速度ay＝0.15g。

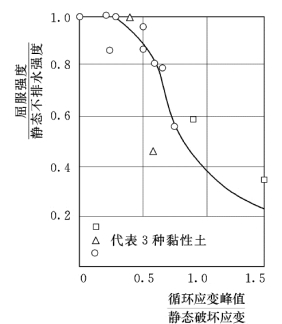
图5.3　屈服强度与循环应变峰值的关系

(www.xing528.com)

图5.4　抗滑稳定安全系数与地震屈服加速度的关系

2.滑动体平均地震加速度的确定

用有限元法进行土石坝动力反应计算，得到各单元的地震加速度反应时程曲线。把滑动体范围内各单元的加速度时程曲线汇总平均，得到平均加速度时程曲线。或者取滑动体重心部位的单元的加速度时程曲线作为平均加速度时程曲线。也可用剪切楔法计算滑动体不同高程的加速度时程曲线，汇总平均得到平均加速度时程曲线。或者用剪切楔法计算滑动体重心高程的加速度时程曲线作为平均加速度时程曲线。

3.永久变形的计算

图5.5 给出了滑动体顺河向平均水平加速度δ··（t）的时程曲线。若滑动体的加速度δ··（t）超过屈服加速度ay，则产生永久变形。将超过屈服加速度ay的平均加速度时程曲线积分得到速度δ·（t）的时程曲线，再将速度时程曲线积分得到位移δ（t）的时程曲线，因此各时段的永久变形为

地震加速度是往复的，当地震反应反向时，若也超过屈服加速度，则在该时段产生反向的永久变形。因此，总的永久变形为各时段变形的累计，即

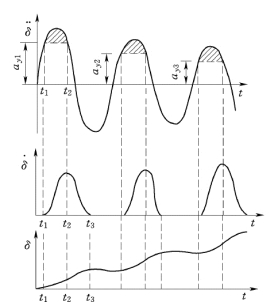
图5.5　永久变形的计算过程

循环次数不同，屈服强度不同，计算得到的屈服加速度也不同。图5.5 是按循环次数不同而不同的屈服加速度ay进行积分的。一般土料，可采用一个不变的屈服强度，因而只有一个屈服加速度。

用类似的方法也可计算土石坝竖向永久变形，为土石坝坝预留地震沉陷超高提供数据。