Finn等 （1980）用内时理论表示循环加荷下饱和砂土的振动孔隙水压力，将孔隙水压力比ud/σ′v与某一单调增长的内时参数k 联系起来。其特点是可以将一组由循环加荷试验得到的孔隙水压力比ud/σ′v与循环振动次数N 关系曲线转换为一条单一的曲线，如图4.42 所示。即ud/σ′v＝G （k），k 是包含剪应变幅值和循环次数的变量，为破损参数。
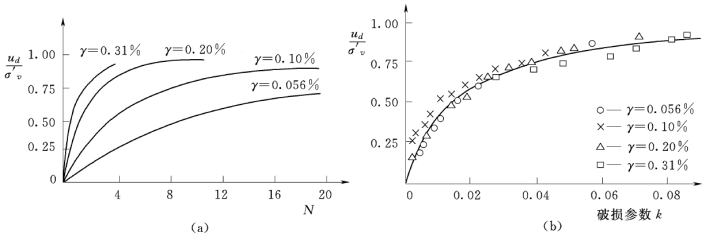
图4.42 循环加荷下振动孔隙水压力比增长曲线
（a）孔压比与循环次数关系；（b）孔压比与破损参数关系
内时理论把土作为非线性弹塑性材料，假设非线性变形和孔隙水压力都是由于土粒在加荷过程中重新排列引起的，而土粒的重新排列由应变路径长度来确定。应变路径长度是一单调递增的函数，称为内时。内时是内时理论的基本参数，用以表示在加荷过程中试样的应变积累，相当于振动N 次剪切时的剪应变，其增量dξ等于偏应变增量，对于单剪试验为
孔隙水压力可表示为
取k＝Tξ，如果对所有的（γ1，ξ1）和 （γ2，ξ2）都能使
(www.xing528.com)
则孔隙水压力比可表示为k 的函数，设
由式（4.23）和式（4.24），得
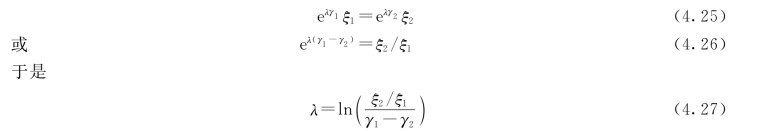
由图4.43 （a）求相应于某一孔隙压力时的 （γ1，ξ1）和 （γ2，ξ2），代入式 （4.27）可以计算λ值。用不同（γ1，ξ1）和 （γ2，ξ2）所计算的λ值相差不大，可取其平均值。λ确定后，由式（4.24）和式（4.23）计算相应于该孔隙水压力的k 值。将ud/σ′v和k 值绘于坐标图上，如图4.43 （b）所示，可将孔隙压力比表示为如下函数
式中 A，B——试验参数。图4.43 所示的试验资料中，A＝111.50，B＝452.46。
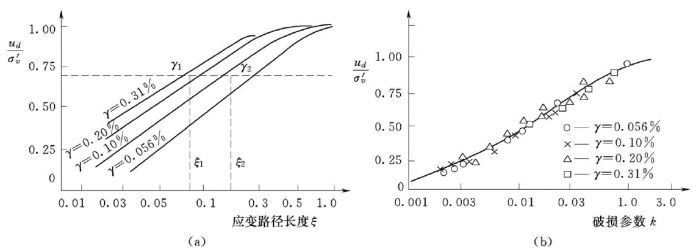
图4.43 振动孔隙水压力的内时模型
（a）孔压比与应变路径长度关系；（b）孔压比与破损参数关系
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
