HardinDrnevich模型详解

Hardin Drnevich模型（1972）假定主干线为一条双曲线（Konder，1963），即

等效线性剪切模量Geq为

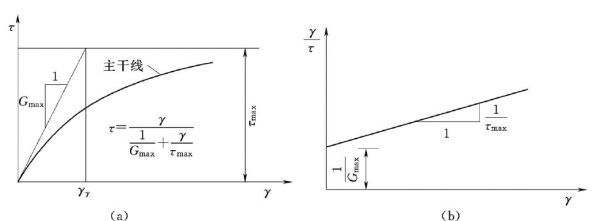
图3.11　Hardin Drnevich模型

（a）主干线；（b）γ～γ/τ关系曲线

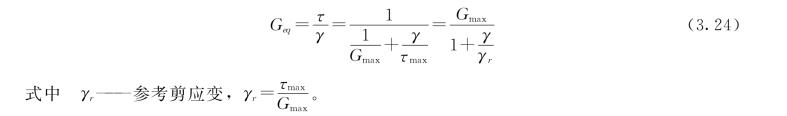
图3.12 为Hardin Drnevich 模型的滞回环，主干线在原点的切线斜率为Gmax。一般开始卸荷时 （A 点）曲线的切线斜率亦为Gmax。Hardin Drnevich模型假定滞回环的面积AL为三角形面积AABC的百分数K1，并认为K1对一种土样的任何滞回环都相同，即

由图3.12 可得

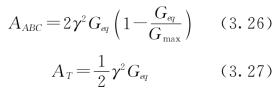
由式（3.25）～式 （3.27）得等效阻尼比λeq为

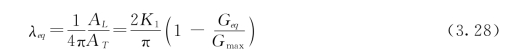(www.xing528.com)

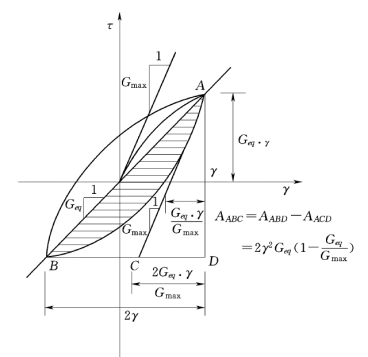
图3.12　Hardin Drnevich模型的滞回环

当γ趋于无穷大时，Geq＝0，故

由式（3.24）、式 （3.28）和式（3.29）得

式中 a、b——系数，取值见表3.1。

表3.1　系数a和b

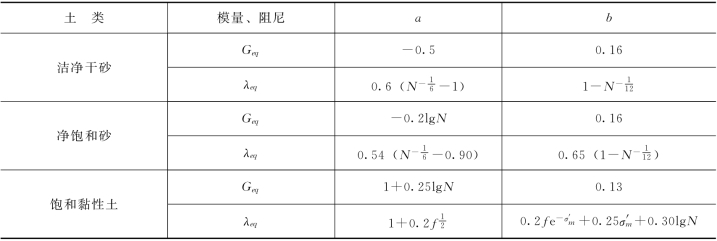
注 N 为振动试验循环次数，对坝址可采用坝址设计地震加速度时程曲线的等效振数；f 为施加振动循环荷载的频率，对坝址可采用设计地震加速度时程曲线的平均频率，单位为Hz；σ′m为平均有效主应力，单位为100kPa，对地基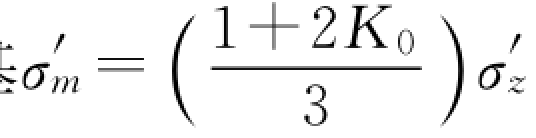，对坝体σ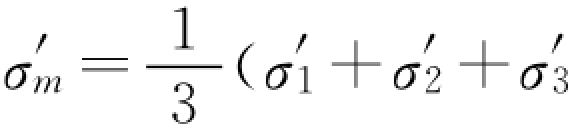），坝体按平面应变问题计算时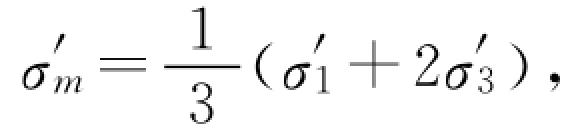，其中σ′1、σ′2和σ′3为有效主应力。

一种土样，在N、f 和σ′m确定的情况下，参数a 和b 的值是常数，可用表3.1 的公式计算。它的Gmax和τmax也是常数，可通过振动单剪试验得到的主干线求得，如图3.11 所示。Gmax还可用现场剪切波测定法确定。因此，γγ是土样的常数，Geq和λeq只随变量γ而变。此外，如没有振动试验或现场波测定资料，Gmax、τmax和λeq，max可用3.5 节经验公式计算确定。