等效线性模型原理介绍

如果在实验室内用振动试验求得的一组应力应变滞回环具有类似于地震的频率，例如1～3Hz，那么这些滞回环可用双线性模型或其他模型来描述，并可应用于地震反应分析中。其中，最简便的是将动应力应变关系用一弹性元件来刻画。图3.4 （a）中的实际动应力应变滞回环近似地等于图3.4 （b）中的等效线性剪切模量Geq加等效阻尼比λeq。

等效阻尼比λeq的表达式为

式中 AL——应力应变滞回环的面积，即一个周期动应变之内的总能量耗散；

AT——图3.4 （a）中三角形OAB 的面积，即等效振动系统的最大能量输入。

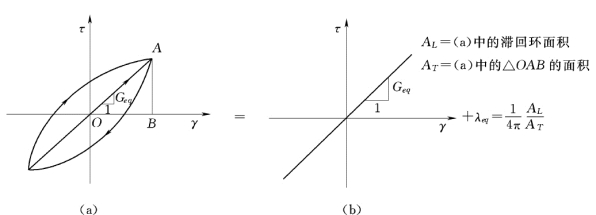
图3.4　等效线性模型

（a）动应力应变滞回环；（b）等效线性剪切模量Geq和等效阻尼比λeq(www.xing528.com)

如果振动试验的振动频率很低 （与地震频率相比），则所得滞回环不包含黏性阻尼。这样所求得的阻尼比偏小，应当用下式修正（Idriss I M，Seed H B）

式中 λvis——黏性阻尼比。

Parmelee等根据自由振动对数衰减率确定的黏性阻尼比为

式中 δi、δi＋1——自由振动中第i 个及第i ＋1 个周期测得的位移振幅。

对于不同的黏性土，λvis的平均值为9.4%。Idriss在其反应分析中采用λvis＝6%。

如果振动试验的振动频率与地震频率相仿，则不必像式 （3.3）那样加上黏性阻尼比λvis进行修正，因为这种滞回环已包含了黏性阻尼、摩擦阻尼和滞变阻尼。