振型组合方式详解

式 （2.174）如以累加公式表示，即

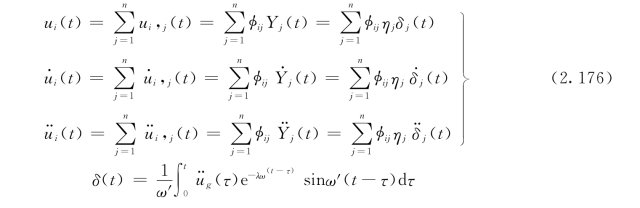
式中 δ（t）——Duhame1 积分；

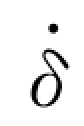（t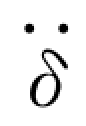）、（t）——上述Duhame1 积分对t 的一阶和二阶导数，见式 （2.172）及式（2.173）；

角标i——质点号；

n——振型的阶数。

应用振型叠加法于实际工程计算时，只需计算前几阶自振频率低的振型累加起来就足以表达体系的振动状态。这是因为：

（1）高阶振型有较多的结点位移为零，即有较多的正负交变。所以高阶振型的振型无量纲值与振型参与系数的乘积[Φ]｛η｝将较小。

（2）高阶振型自振频率高，自振频率很大时，该振型所对应的“单质点”的加速度反应接近于地面运动加速度，位移反应因此位移反应较小。而低阶振型的 “单质点”加速度反应对地面运动加速度将有一定的放大，且频率ω又较低，故位移反应较大。

从物理意义上看，由地面运动激发结构体系的振动过程中，高阶振型的振动不太容易激发。

在计算时取振型数的多少，还要考虑以下两个因素：

（1）体系自振频率谱的分布。若体系的自振频率较低，将有较多个振型容易被地面运动激发，需要考虑计入的振型数要多一些。反之，若体系的自振频率较高，则考虑计入的振型数可少一点。另外，如果结构体系的自振频率分布较密，即相邻振型的相差较小，则考虑计入的振型数要多一些。反之，自振频率分布较疏，则考虑计入的振型数可少一些。例如拱坝要多算几个振型，重力坝、土石坝可少算几个振型。

（2）地面运动的频谱特性。若输入的地面运动加速度过程线中高频分量较多，对高振型的激发就较为显著，需要考虑计入较多个振型。反之，地面运动加速度过程线中高频分量较少，则可考虑计入较少振型。一般地说，浅震和近震的地面运动加速度过程线中，卓越周期较短，需考虑计入的振型数应多一些。反之，深震和远震的地面运动卓越周期较长，需考虑计入的振型数可少一些。

根据实际计算经验，土石坝和混凝土重力坝用振型叠加法分析时，计算3～5 个振型即可，而混凝土拱坝则需计算6～10 个振型。

式中 Sd，n、Sv，n、Sa，n，re——第n 阶振型相对位移反应谱值、相对速度反应谱值、相对加速度反应谱值。

几个振型的最大反应值如何组合成多质点体系的最大反应值，有以下几种方式（以相对加速度反应为例，其他物理量类推）：

(www.xing528.com)

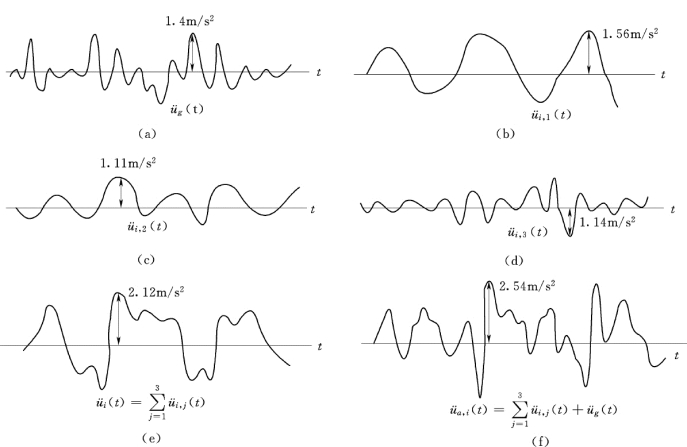
图2.27　三阶振型的叠加

（1）方式一：

式中 as——振型耦合系数，一般采用0.3、0.4、0.5，由于统计资料不多，难以确定as之值。

以上讨论的是相对反应值的组合问题，关于绝对反应值的组合，还存在着不同的观点。

多质点体系质点i 的绝对加速度反应值为

式 （2.181）表示各振型的相对加速度反应时程曲线叠加起来，再与地震加速度时程曲线叠加，便得到绝对速度反应时程曲线。此曲线上的最大值便是最大绝对加速度反应值。例如图2.27 （b）、（c）、（d）3 条曲线叠加便得到相对加速度反应时程曲线 （e）。将曲线（e）与曲线（a）（地震加速度时程曲线）叠加便得到绝对加速度反应时程曲线 （f）。此曲线上的最大值ua，i，max＝2.54m/s2是最大绝对加速度反应值。

为了计算简便，用抗震规范推荐的设计反应谱计算各阶振型的加速度反应值时，需要利用绝对加速度系数反应谱值β。各振型的最大绝对加速度反应值为

用式（2.182）计算各振型的最大绝对加速度反应值以后，如何组合成多质点体系的最大绝对加速反应值，有以下两种常用方法。

（1）第一种方法：

上式采用与相对加速度反应组合相同的 “平方和的开方”的方法。但建筑物的底部φn＝0，以致底部的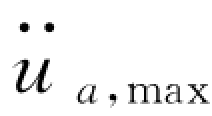＝0，这是不合理的。

（2）第二种方法：