运动方程的描述和应用

多自由度体系的运动方程为

用基准位移除式（2.130）两边，得

在无阻尼条件下，式 （2.165）退化为

式 （2.165）和式（2.166）分别是有阻尼和无阻尼条件下第n 阶振型的单自由度方程。

对于多自由度体系的每一个振型，都用上述方法求得一个独立的单自由度方程。因此，用正则坐标可以将n 个联立微分方程转换成n 个独立的正则坐标方程，如式（2.165）或式（2.166）。可以用2.2 节单自由度体系的数值积分法求广义坐标的反应Yn（t）。求出Y1（t）、Y2（t）、…、Yn（t）后，再用式 （2.154）计算多自由度体系各质点的位移反应u1（t）、u2（t）、…、un（t），这种方法称为“振型叠加法”。

【例2-7】 仍用[例2-5]中图2.21 （a）所示框架及劲度影响系数的数据，假定结构无阻尼，用振型叠加法求自振位移反应和速度反应。初始条件为

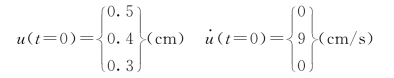
求由初始条件产生自由振动的位移反应。

解：利用[例2-5]的计算成果，有(www.xing528.com)

按式（2.157）的形式，对应于初始位移的广义坐标为

将已知数据代入上式，得

广义坐标的自由振动反应与单自由度体系的自由振动反应式（2.5）相同，故

由此，把上面求得的广义坐标的初始条件和振型频率代入上式，得到各振型的广义坐标自振反应为

体系各质点的自振反应由振型[φ]乘广义坐标Y （t）叠加得到，故

可见，每一质点的位移反应和速度反应都包含结构各个振型的贡献，高阶振型的贡献比低阶振型的贡献小。