【摘要】:图2.23两个振型和惯性力图2.23 表示一个结构体系的两个不同振型:m 阶振型和n 阶振型。由式可知式等号右面等于零,故得到第二个正交条件式 和式采用无量纲振型向量表示,等式仍成立。这样振型的正交条件成为振型的正交性在动力分析中有很大用处,对于相同频率的两个振型,正交性不适用。解:由 [例2-5]得用一阶振型和二阶振型验算,即满足正交性条件。
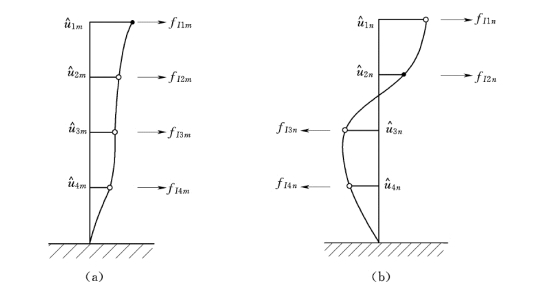
图2.23 两个振型和惯性力
图2.23 表示一个结构体系的两个不同振型:m 阶振型和n 阶振型。体系自由振动的运动方程式(2.115)可写成
![]()
式 (2.130)右边表示施加的惯性力荷载 {fI},左边表示弹性恢复力 {fs}。因此,可以把自振运动当作以惯性力为作用荷载而产生位移,如图2.23 所示。这样,图2.23 中的两个振型就是两种不同荷载作用在同一体系上所产生的两种位移。根据虚功原理得
![]()
把式(2.130)中的惯性力向量代入式(2.131),得

因为ωm≠ωn,故必须

这是第一个正交条件。
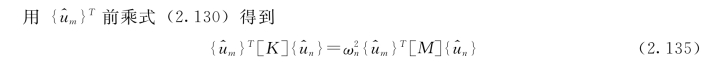
由式(2.134)可知式(2.135)等号右面等于零,故得到第二个正交条件(https://www.xing528.com)
![]()
式 (2.134)和式(2.136)采用无量纲振型向量表示,等式仍成立。这样振型的正交条件成为
![]()
![]()
振型的正交性在动力分析中有很大用处,对于相同频率的两个振型,正交性不适用。
由于假定阻尼矩阵是质量矩阵和劲度矩阵的线性函数,故正交条件也适用于阻尼矩阵,即
![]()
【例2-6】 用 [例2-5]中所示的框架 [图2.21 (a)],3 个无量纲振型如图2.22所示,验算是否满足对质量和劲度的正交性。
解:由 [例2-5]得

用一阶振型和二阶振型验算,即

满足正交性条件。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




