【摘要】:同样,把ω2、ω3代回式,可求得故无量纲振型为如果有n 个质点,则振型方阵为 如图2.21所示的结构,假定横梁是刚性的,柱的弹性系数和横梁的质量见图中数据,各质点的劲度影响系数的求法如图2.21所示,试求解该结构的自振频率和振型。因此该结构的自振频率为:ω1=14.522rad/s,ω2=31.048rad/s,ω3=46.100rad/s。图2.22框架的振型

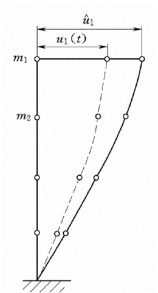
图2.20 多自由度体系在时刻t 的振动形状
将式(2.119)分块成下列两式

式 (2.120)是多余的,但可用来校核计算成果的正确性。
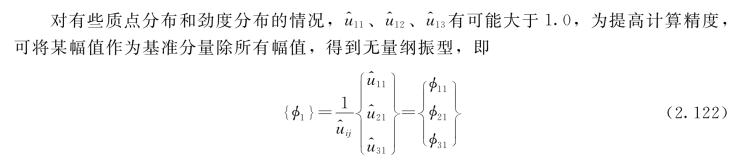
同样,把ω2、ω3代回式(2.115),可求得
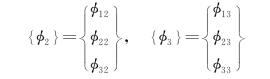
故无量纲振型为

如果有n 个质点,则振型方阵为

【例2-5】 如图2.21(a)所示的结构,假定横梁是刚性的,柱的弹性系数和横梁的质量见图中数据,各质点的劲度影响系数的求法如图2.21(b)所示,试求解该结构的自振频率和振型。
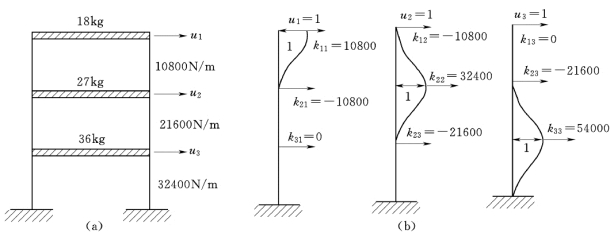
图2.21 自振频率计算(https://www.xing528.com)
(a)框架体系;(b)劲度影响系数
解:由图2.21 (a)可得框架结构的质量矩阵和劲度矩阵为
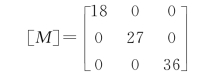

令式(2.125)矩阵的行列式为零,即det([K]—ω2[M])=0,得
![]()
求解上述方程,得:B1=0.35146,B2=1.60660 和B3=3.54194。因此该结构的自振频率为:ω1=14.522rad/s,ω2=31.048rad/s,ω3=46.100rad/s。
振型方程为
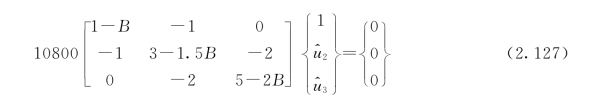
除以基准量10800,并写成分块阵,得

将一阶振型B1=0.35146 代入式(2.129),解得Φ21=0.64853,Φ31=0.30185。用式(2.128)校核,证明无误。类似地,二阶振型:Φ22=—0.60660,Φ32=—0.67898;三阶振型:Φ23=—2.54185,Φ33=2.43954。振型方阵为

本题中已令Φ11、Φ21、Φ31都等于1.0。这个框架结构的3 个振型如图2.22 所示。
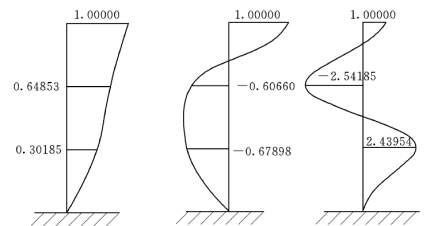
图2.22 框架的振型
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




