使用增量方程式求解非线性单自由度体系的反应

图2.17 （a）为非线性单自由度体系，图2.17 （b）为动力系统平衡图，图2.17 （c）、图2.17 （d）、图2.17 （e）、图2.17 （f）分别为弹性恢复力、阻尼力、惯性力、地震加速度的非线性曲线。

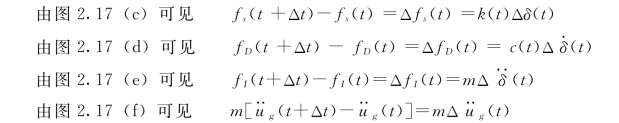
则增量形式的运动方程为

下面以Wilson—θ法为例，推导增量形式的运动方程的地震反应计算公式。由式（2.62）

令τ＝t＋Δt，代入上式，整理后得

由式（2.67）～式 （2.69），可得

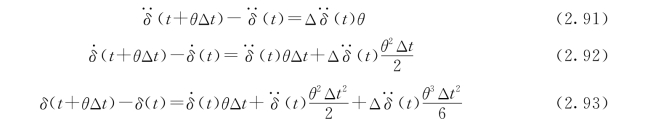
将式（2.90）分别代入式（2.91）～式 （2.93），得

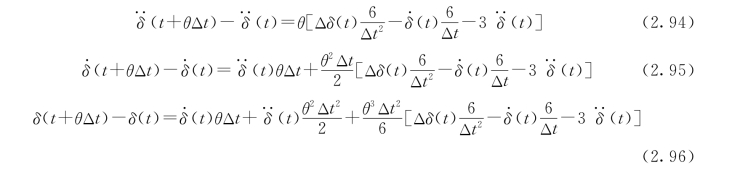
将t＋θΔt 时刻和t 时刻的运动方程相减得到下列增量方程式

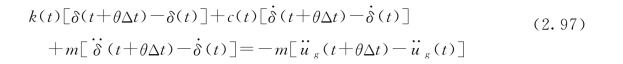
将式（2.94）～式 （2.96）代入式（2.97），整理后可得

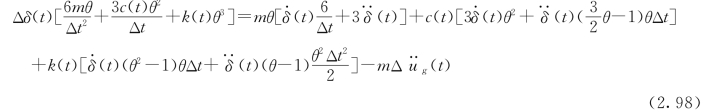
上式可写成

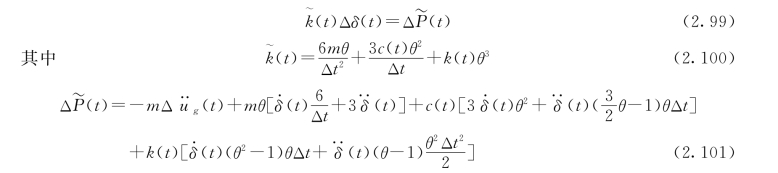
式（2.100）称为等效劲度，式 （2.101）称为等效荷载增量。当θ＝1，式 （2.99）～式（2.101）退化为增量形式的线性加速度法的计算公式。

主要计算步骤如下：

（1）对任一给定的时间增量，起始时刻的速度和位移是已知的，它们或是给定的初始条件或是前一增量终点处的值。

（2）利用这些已知值和结构的非线性曲线，求出时间间隔内的阻尼系数c（t）和劲度k（t），以及阻尼力fD（t）和弹性恢复力fs（t）的值。c（t）和k（t）可用曲线上时间间隔起点的切线斜率，如图2.17 所示。(www.xing528.com)

（3）根据运动方程，某时段起点的初始加速度由下式计算

（4）由式（2.100）计算等效劲度~k（t），式 （2.101）计算等效荷载增量Δ～P（t），用式（2.99）计算位移增量Δδ（t），由下式求速度增量

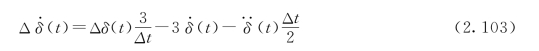
（5）由式（2.104）和式（2.105）计算该时段终点时的速度和位移

【例2-4】 如图2.18 （a）所示，体系的质量和阻尼系数为常量，劲度系数在弹性阶段为1.0 N/cm，在塑性阶段为零。弹性恢复力fs～δ关系示于图2.18 （b）。图2.18 （c）给出了地震加速度时程曲线的一部分。试用增量方程式计算体系的地震反应。

解：主要计算公式见式（2.99）～式 （2.101），取θ＝1，即为线性加速度法的计算公式。取Δt＝0.01s。

由式（2.100），等效劲度为

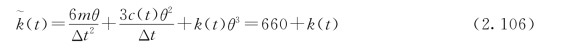
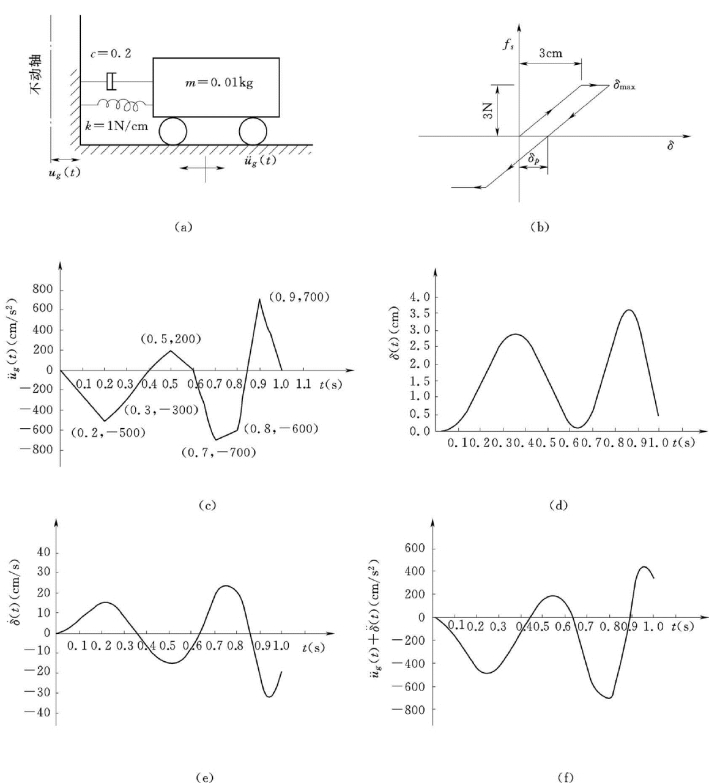
图2.18　弹塑性体系地震反应计算

（a）单质点体系；（b）fs～δ关系曲线；（c）地震加速度时程曲线；（d）位移反应过程线（e）速度反应过程线；（f）绝对加速度反应过程线

由式（2.101），等效荷载增量为

由式（2.103）计算的速度增量为

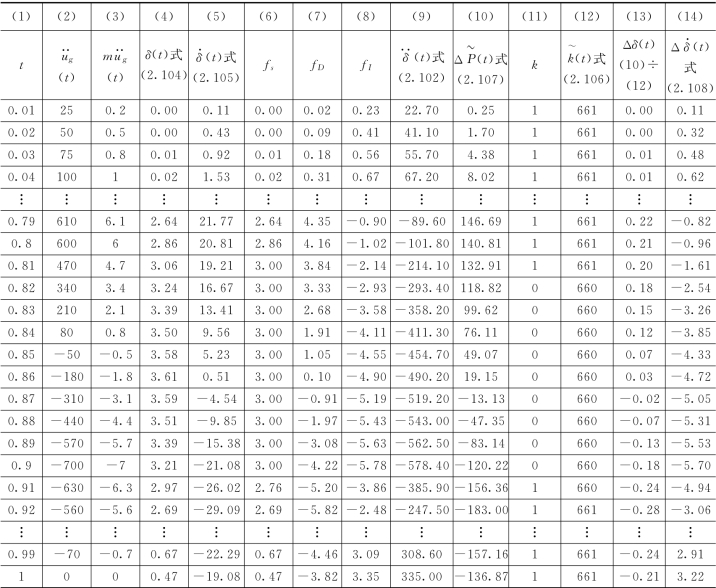
主要计算过程列于表2.5，其中表中 （10）～ （14）栏得到的计算结果Δδ（t）和Δ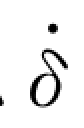（t）用于计算该时刻（4）～ （5）栏的δ（t）和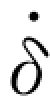（t）。由表2.5 可见，在0.81s 时，δ＝3.06cm，超过了弹性极限位移3cm，表明体系已屈服，进入塑性状态。在进行下一时段计算时，取劲度系数k＝0，弹性恢复力fs＝3 N。当体系从0.90s 进入到0.91s 时，位移从3.21cm变为2.97cm，表明体系从弹塑性状态返回至弹性状态，其中塑性残余位移为3.21—3＝0.21cm，因此在0.91s时，恢复力fs＝（2.97—0.21）×1＝2.76N。

本例中fs与δ是线性关系，对于非线性情况，计算过程完全类似，只需在每个时段对劲度k 进行相应的更新即可。

表2.5　弹塑性体系地震反应计算表