【摘要】:Wilson—θ法是对线性加速度法的改进,它假定加速度在θΔt 时段内呈线性变化,因此亦称为超前线性加速度法。 单质点体系的特性及地震加速度过程线与 [例题2-1]相同,试用Wilson—θ法求该体系的位移反应、速度反应和加速度反应。取Δt=0.005s,θ=1.4,则将β、θ、ω、λ的值分别代入式、式 和式,得主要计算过程见表2.4。表2.4Wilson—θ法计算体系的地震反应
Wilson—θ法是对线性加速度法的改进,它假定加速度在θΔt 时段内呈线性变化,因此亦称为超前线性加速度法。选择合适的θ可以保证计算过程的稳定性和计算成果的一定精度。研究表明,只要θ≥1.37,计算是无条件稳定的。当θ=1 时,就退化为线性加速度法。
令式(2.60)~式 (2.62)中的τ=t+θΔt,可以得到
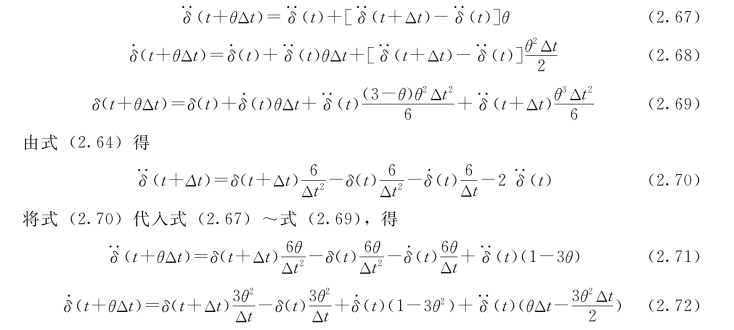
![]()
将式(2.71)~式 (2.73)代入t+θΔt 时刻的运动方程
![]()
整理后得
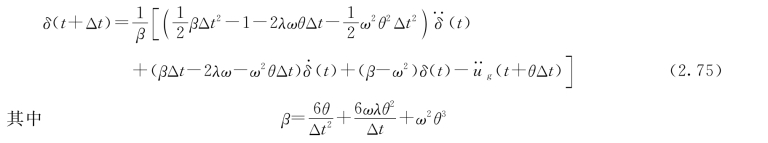
将式(2.75)代入式(2.70)可得
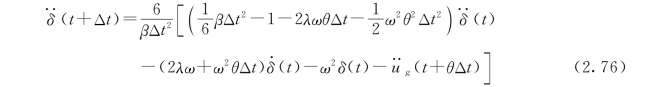
将式(2.76)代入式(2.63)可得(https://www.xing528.com)
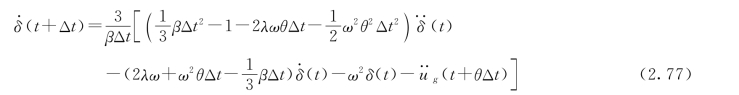
计算时先确定Δt 和θ,则常数β便可计算出来。式 (2.75)~式 (2.77)中的系数都是常数,则时刻t+Δt 的加速度、速度、位移反应便可由已知的上一时刻t 的加速度、速度、位移反应以及由地震加速度时程曲线上查得的时刻t+θΔt 的地震加速度等数值计算得到。逐次递推下去,便可求得体系在整个地震过程中的反应过程线。为使解答达到一定精度,时间步长Δt 仍以小于体系自振周期的1/10 及地震卓越周期的1/5为宜。
【例2-3】 单质点体系的特性及地震加速度过程线与 [例题2-1]相同,试用Wilson—θ法求该体系的位移反应、速度反应和加速度反应。
解:由 [例2-1]得:ω=22.15rad/s。取Δt=0.005s,θ=1.4,则
![]()
将β、θ、ω、λ的值分别代入式(2.75)、式 (2.77)和式(2.76),得

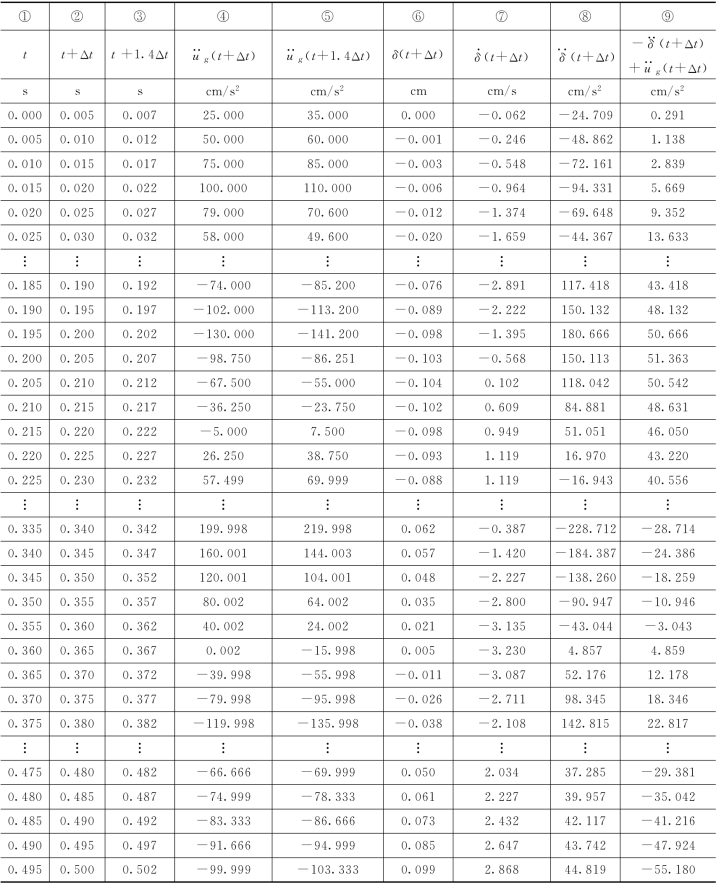
主要计算过程见表2.4。
表2.4 Wilson—θ法计算体系的地震反应
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




