阻尼体系对地震反应的影响

有阻尼单自由度体系的地震位移反应见式（2.26）。将式（2.26）改写成如下形式

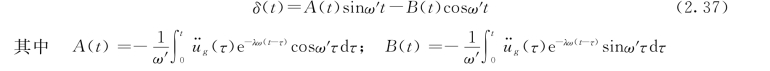
与无阻尼的情况类似，同样可用图2.8 的作图方法，但图2.8 （b）的cosωτ改为cosω′τ，则y（τ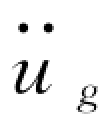）＝（τ）cosω′τ，三种求和方法的A（tn）分别为

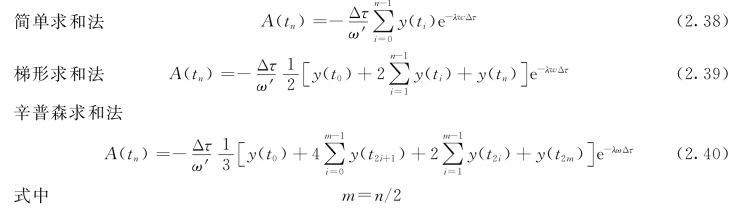
此处n 要求为偶数。

用同样方法求B（t），最后便可求得各时刻的相对位移反应，即

据此可以作出相对位移反应过程线，并得到最大反应值。相对位移与地震的地面运动位移之和称为绝对位移反应。

对位移反应式（2.37）[即式（2.26）]关于t 求一阶导数可得体系的相对速度反应，即

根据运动方程式（2.23），体系的绝对加速度反应为

将式（2.42）代入式（2.43），得体系的绝对加速度反应为

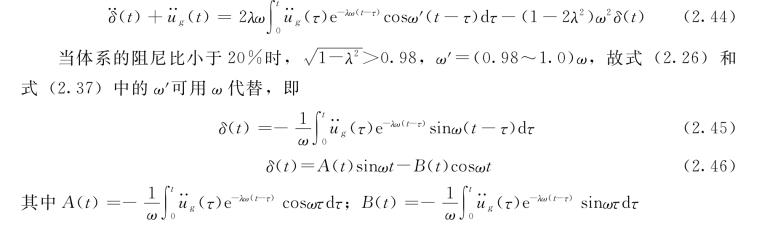
同样，速度反应和绝对加速度反应仅需将式（2.42）和式（2.44）中的ω′用ω代替即可。

在作数值积分求解地震反应时，时间步长Δτ （图2.8）应远小于体系自振周期和地震卓越周期，可取等于地震卓越周期的1/5～1/10，常取步长为0.01s。

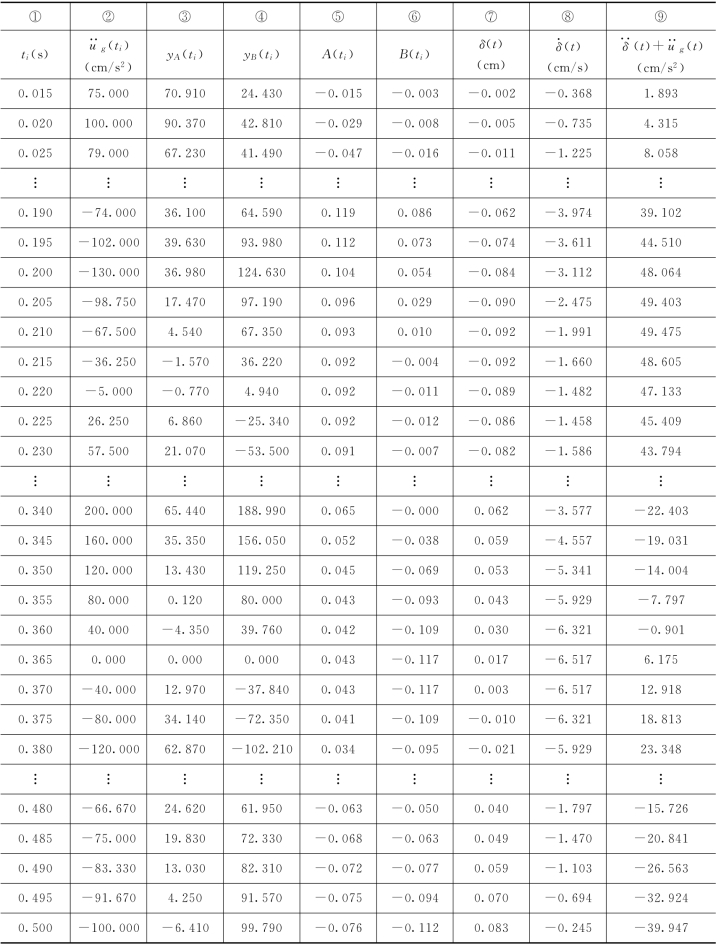
【例2-1】 有一单质点体系，质量m＝15kg，劲度系数k＝7357.5N/m，阻尼比λ＝0.05，地震加速度时程曲线如图2.9（a）所示，求体系的位移反应、速度反应和加速度反应。(www.xing528.com)

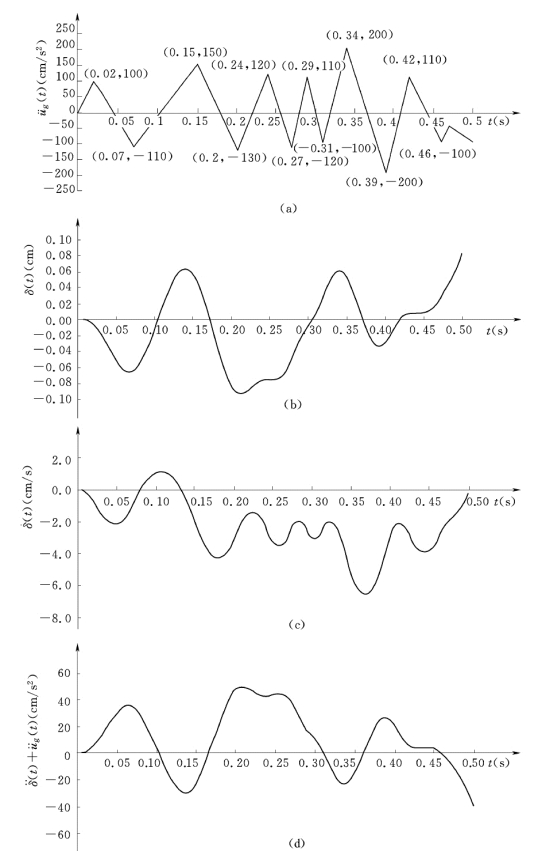
图2.9　地震加速度时程曲线和地震反应过程线

（a）地震加速度时程曲线；（b）位移反应过程线；（c）速度反应过程线；（d）绝对加速度反应过程线

解：

由式（2.41）计算位移反应，即

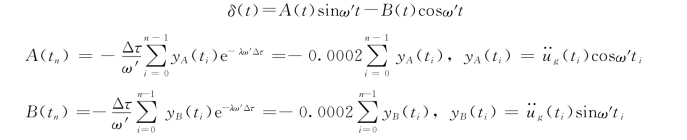
由式（2.42）计算速度反应，即

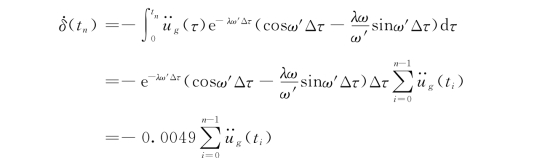
由式（2.43）绝对加速度反应，即

位移反应、速度反应和绝对加速度反应过程线分别见图2.9（b）、图2.9（c）和图2.9（d）。

表2.2　地震反应计算表

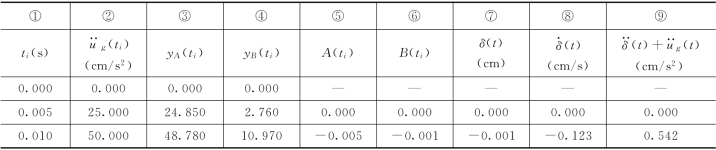
续表