【摘要】：无阻尼 的单自由度体系的地震反应公式可由式得将sinω（t—τ）用三角公式展开，式 可写成为了计算式的数值积分，首先要对A和B进行数值积分，以A 为例进行说明。将时间t 等分成几份，得到等时间步长Δτ＝ （t/n）。将被积函数绘于图2.8 和图2.8 ，把图2.8 和图2.8 两曲线互相对应的纵坐标相乘得y（τ）＝（τ）cosωτ，绘于图2.8 。
对于一个很短暂的冲击荷载，在最大反应出现之前，阻尼力还来不及从建筑物吸收较多的能量，所以可以当作无阻尼体系计算。对于无阻尼体系，λ＝0，ω′＝ω，故式（2.27）成为
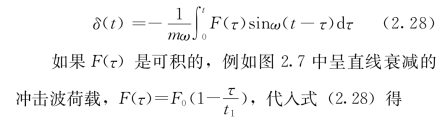
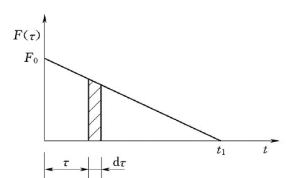
图2.7 冲击荷载形式
将式（2.29）积分，并注意到mω2＝k，得
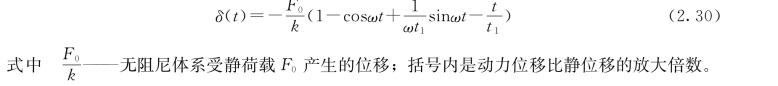
地震荷载过程是复杂的函数，不能直接积分，只能用数值积分法求解。无阻尼 （λ＝0，ω＝ω′）的单自由度体系的地震反应公式可由式（2.26）得
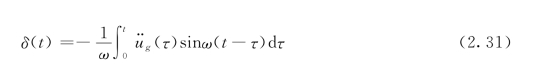
将sinω（t—τ）用三角公式展开，式 （2.31）可写成
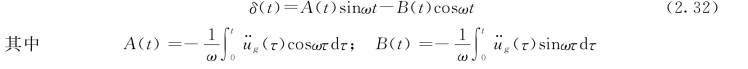
为了计算式（2.32）的数值积分，首先要对A（t）和B（t）进行数值积分，以A （t）为例进行说明。将时间t 等分成几份，得到等时间步长Δτ＝ （t/n）。将被积函数绘于图2.8 （a）和图2.8 （b），把图2.8 （a）和图2.8 （b）两曲线互相对应的纵坐标相乘得y（τ）＝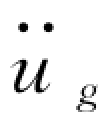
（τ）cosωτ，绘于图2.8 （c）。(www.xing528.com)
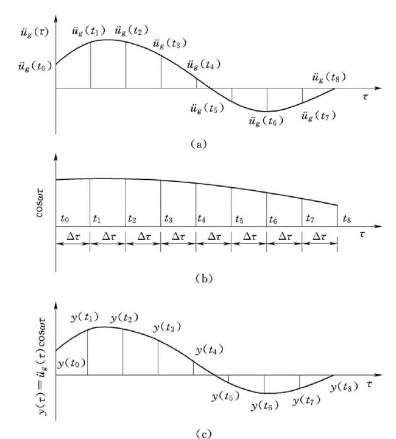
图2.8 杜哈姆积分的数值求和法
如用简单求和法，则
如用梯形求和法，则
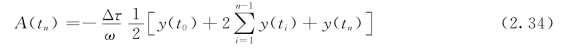
如用辛普森（Simpson）求和法，则
此处n 要求为偶数。
用同样方法求B（t），最后便可求得各时刻的相对位移反应
由此可以作出相对位移反应时程曲线，并得到最大位移反应值。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
