【摘要】：地震作用下单质点体系的运动方程为式 是一个二阶常系数非齐次线性微分方程，其通解为式 右边第一项是体系自振运动方程的解，第二项是体系强迫振动运动方程的一个特解。可以将地震加速度时程曲线划分成微条，如图2.6 所示，微条的面积作为初始速度，用式 （2.9）计算各初速作用后在时间t 的反应，将所有初速作用后在时间t 的反应累加起来就是地震荷载作用在体系的反应。
式 （2.23）是一个二阶常系数非齐次线性微分方程，其通解为
式 （2.24）右边第一项是体系自振运动方程的解，第二项是体系强迫振动运动方程的一个特解。将地震开始前体系的初始条件代入式（2.9），得自振运动项为零，因此只需求解强迫振动的特解η（t）即可。
由于地震加速度时程曲线u··g（t）是一条很复杂的曲线，很难用简单的函数表达，因此无法求得η（t）的解析解。可以将地震加速度时程曲线划分成微条，如图2.6 所示，微条的面积作为初始速度，用式 （2.9）计算各初速作用后在时间t 的反应，将所有初速作用后在时间t 的反应累加起来就是地震荷载作用在体系的反应。
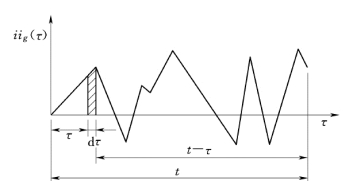
图2.6 地震反应计算示意图(www.xing528.com)
图2.6 中阴影微条的横坐标为τ，纵坐标为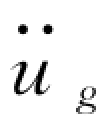
（τ），宽度为dτ，面积近似地等于
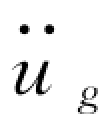（τ）dτ，这面积是在时刻τ作用在建筑物的速度增量，在每一瞬时建筑物都受一速度增量的作用。上述速度增量可当作建筑物在瞬时τ所获得的初速，按式（2.9）计算其在时间t 的反应（初位移δ0＝0）
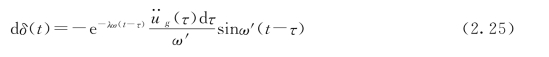
图2.6 所有微条的面积在不同的时间τ作为建筑物的初速，到时间t 发生的相对位移反应为
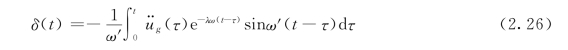
这个积分称为杜哈姆积分（Duhamel Integral）。
如果纵轴是图2.7 中的冲击力F（τ），则位移反应为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
