阻尼力、阻尼系数和阻尼比的含义及作用

阻尼力是阻碍质点运动的一种力，它和

质点运动的速度方向相反。阻尼力有以下几种类型：

1.摩擦力

这种阻尼力发生在固体相互摩擦处，例如在结构的构件连接处，砂土颗粒间的摩擦等。这种阻尼力与运动的速度无关，但与应力有关。对运动速度来讲，它是常量，即

式中 c1——摩擦阻尼力；

A——接触面积；

σ——压应力；

φ′——有效摩擦角。

式中正负号的取法应使FD与速度方向相反。

2.黏性阻尼力

这种阻尼力发生在固体相互接触但有润滑剂存在的部位。此外，某些黏弹性材料，如黏土、砂土、混凝土等，发生变形时，产生抵抗力。这种抵抗力，包括与变形成正比的弹性力及与速度成正比的黏性阻尼力。黏性阻尼力可表示为

式中负号表示阻尼力的方向与运动速度方向相反。

3.流体动力

当固体在水或空气中运动时，受到这些流体动力的阻力。这种阻尼力与运动速度的平方成正比，其方向则与速度的方向相反，即

4.其他类型的阻尼力

其他类型的阻尼力中，最重要的是滞变阻尼力。弹性体受外力发生变形时，如果外力是静荷载 （即加荷速度很慢），则抵抗力与变形成正比，即Fs＝kδ，k为劲度系数，δ为变形，如图2.5 中直线AC。当逐级加荷速度很快，抵抗力与变形的关系成滞回线，如图2.5 中ABCDA。如果材料不是纯弹性体，这个滞回环就包括滞变阻尼、黏性阻尼和摩擦阻尼，砂土、黏土就属此类型。图2.5 中EG 表示弹性力Fs，HE 表示阻尼力FD。

体系振动时，为了克服阻尼力，就需外力作功。这个功等于阻尼力发生的能量损耗。阻尼力发生的能量损耗较难计算，但其中黏性阻尼力发生的能量损耗，计算比较简便。如果把所有的阻尼力发生的能量损耗都当作黏性阻尼力的能量损耗，这样求出来的阻尼力就称等效黏性阻尼力。

有阻尼体系的自由振动的振幅是逐渐衰减的，如图2.3 所示。计算振动一周所损耗的能量时近似地认为在一周内振幅衰减不大，即假定δ2＝δ1，故仍按简谐振动考虑。

(www.xing528.com)

黏性阻尼体系振动时，时间t1→t2，发生变形δt1→δt2，其能量损耗为

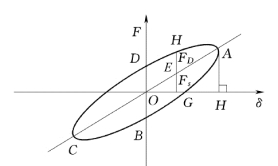
图2.5　F～δ滞回环

图2.5 中滞回环ABCDA 可由试验得到，滞回环所包的面积为包括各种阻尼在内的阻尼损耗的能量。直角三角形OAH 的面积为最大变形能。阻尼能量损耗与最大变形能之比为

式中 AL——滞回环的面积；

AT——三角形OAH 的面积。

如果令所有阻尼能量损耗等效于黏性阻尼能量损耗，即

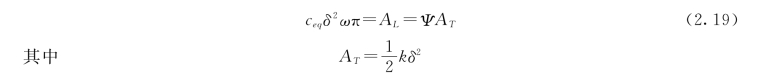
式中 ceq——包括滞变和摩擦在内的等效于黏性阻尼的系数，称为等效黏性阻尼系数。对于单质点体系，k＝mω2，代入式（2.19），得

等效黏性体系的阻尼比为

式中 ccr——临界阻尼系数。

单质点体系的ccr＝2mω，代入式（2.21）得

一般土建结构，当振动应变水平较小和振动频率较小时，Ψ值及λeq值见表2.1。

表2.1　建筑材料或建筑物的Ψ值和λeq值

在振动应变水平较大时，表中混凝土拱坝、混凝土重力坝、土石坝的等效阻尼比λeq可取上限值。