确定非平稳模型的待定参数

为了较好地描述地震地面运动从开始、强震段、然后自然衰减的全过程，一般采用非平稳模型。目前用非平稳随机过程模拟地震地面运动的一个比较实用的方法，是将白噪声或有色噪声通过能反映地基特性的滤波器滤波后，再乘上表示非平稳性的确定性函数。这样建立的地震地面运动加速度的非平稳模型可以表示为

式中 f（t）——反映地震动从开始经强震段到衰减的强度 （均方差）变化过程的确定性函数，简称为非平稳强度函数；

A（t）——上面给出的平稳过滤有色噪声。

地面运动非平稳性的确定性函数f（t），其表达式有多种取法，现采用如下常用的典型函数

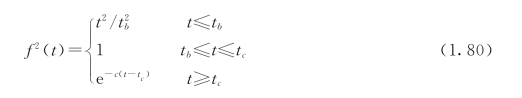
式中 tb、tc、c——控制主震段首末时间和衰减快慢的参数，如图1.36 所示，这里取c＝0.18。图中Tc＝tc—tb是强震平稳段的持续时间。

表1.17　包线参数值

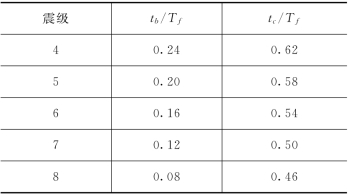
图1.36　非平稳强度函数f（t）的形状

文献[23]给出了tb及tc的取值，见表1.17。其中Tf为非平稳地震动持时。

震级与烈度的关系^[3]可以表示为

地震动非平稳模型的功率谱密度可以表示为

加速度过程的方差可以写成

式中 ——平稳过程的方差。

地震动非平稳模型对应的地震持续时间Tf的确定可以由平稳模型的持时直接得到。

将式（1.83）代入式（1.66）可得(www.xing528.com)

将式（1.84）代入式（1.65）得

比较式（1.68）和式（1.85），就可得到确定Tf的方程

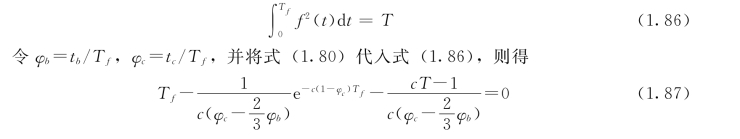
求解方程式（1.87）就可得与烈度及场地土对应的地震动非平稳持时Tf，结果列于表1.18。

从表1.18 中可见，非平稳持时亦随烈度增大而增大，随场土变软而变大；比较表1.16 及表1.18 的结果可以看出，地震动非平稳持时较平稳持时为大，这是合理的。

根据文献[13]，参数tb和tc还可按如下定义确定

表1.18　不同烈度、不同场地的Tf

式中 E（t）——地震动在（0，t）时段内的能量；

E（∞）——地震动的总能量。

式 （1.88）表明：tb规定开始段占总能量的10%；tc规定衰减段占总能量的20%。

取E（∞）为平稳地震动的总能量，即

则按式（1.88）的能量分配原则，可以求得

因此，对于非平稳模型式（1.79），没有特别需要确定的参数。

上述的平稳和非平稳模型同时适用于水平和竖向地震动，只是模型中的参数应按水平和竖向的情况相应确定。