1.以MM烈度表的物理量统计关系为基础，确定地震动持时和谱强度因子
人们通过大量强震记录的分析和地震动特征的研究，提出了多种模拟地震动的平稳随机过程模型。其中，日本学者金井清（1987）（见文献[15]）提出的平稳过滤白噪声模型颇具代表性。该模型的谱密度函数表达式为
式中 S0——基岩白噪声谱密度；
ξg、ωg——地表覆盖土层的阻尼比和卓越频率。
式 （1.51）是将地表覆盖土层视为单自由度线性滤波器，由基岩白噪声通过滤波得到的结果。它具有物理意义明确的特点，同时也考虑了地基土特性对地震地面运动的影响。
但是，由于金井清的模型假定了基岩地震动为白噪声，因此，它不能反映基岩地震动的频谱特征；此外，由该模型不能求出地面位移、速度及加加速度（即加速度的导数）均方差的有限值。
为了保持金井清谱过滤噪声的特点（即把地表覆盖土层处理为单自由度线性滤波器）并克服金井清的上述缺陷，将基岩加速度谱假定为马尔柯夫有色谱，其谱密度可以表示为
式中 ξg、ωg——地表覆盖土层的阻尼比和卓越频率；
SI（ω）——基岩地震加速度J（t）＝
（t）的谱密度，可以表示为式 （1.53） （金井清，1987，见文献[15]）。
式中 S0——引起基岩运动的随机激发 （白噪声）的白谱，它是反映地震动强弱程度的因子，简称为谱强度因子；
ωh——反映基岩特性的谱参数，文献[13]、[15]建议取ωh＝8πrad/s。
将式（1.53）代入式（1.52）可得
由式（1.54）能够求得地面加速度及加加速度的有限值，称式（1.54）为平稳高斯过滤有色谱模型。
目前工程抗震设计都是以地震烈度来衡量一次地震的强弱程度。因此为了将结构的随机地震效应分析结果应用于结构抗震设计，进一步完善结构抗震设计理论，就必须建立地震动参数（谱强度因子S0及地震持续时间T）与地震烈度的联系。
由随机振动理论可知，地面加速度过程及加加速度过程的方差可以表示为
将式（1.54）代入式（1.55）和式（1.56），进行积分则得
为地面加速度过程的最大值。由随机极限值理论，对于平稳高斯过程，其最大值的均值可以表示为
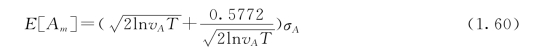
式中 T——地震持续时间；
σA——地面加速度过程的均方差；
vA——地面加速度过程的越零率 （信号之振幅通过零点之次数，越零点的值越多，就表示所处理的信号频率越高，反之则表示所处理的信号为低频）。
令E[Am]等于与地震烈度对应的地面加速度最大值的统计平均值am（I），则得
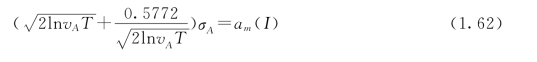
实际上，影响地面加速度最大值的因素很多，除地震烈度外，场地土的卓越周期对其有显著的影响。文献[15]给出了由地震烈度（MM烈度）与场地土卓越周期Tg确定的加速度最大值的经验公式为
(www.xing528.com)
式 （1.62）是关于地震持时T 及谱因子S0（σA）的一个方程。令
文献[17]由统计分析给出了IA与地震烈度（MM烈度）的关系方程，可表示为
文献[18]指出，MM烈度大致与我国的烈度相近。
对式（1.64）两边取均值，可得
将式（1.67）代入式（1.65），可得S0与T 的第二个方程
由式（1.57）知
联解式（1.62）及式（1.68），则得确定地震动参数S0及T 的关系式
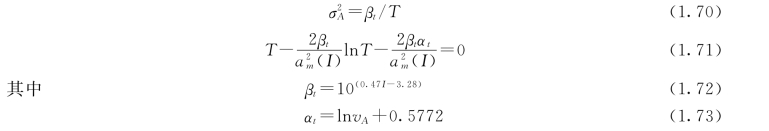
利用式（1.69）～式 （1.73）就可得到不同烈度、不同场地土类别对应的地震动参数S0及T。
表1.15 给出了四类场地土的卓越频率及阻尼比 （见文献 [18]）。由于目前有关场地土阻尼比的资料有限，表1.15 中的阻尼比是参考文献[19、21]假定的值。
表1.15 场地土参数
表1.16 列出了我国抗震规范给出的远震前三类场地土求出的Ⅳ～Ⅸ度时T 及S0的结果。
表1.16 不同烈度、不同场地的T及S0值
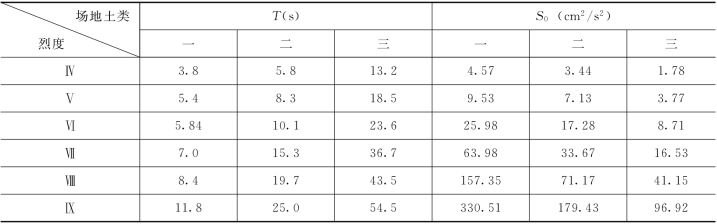
从表1.16 可以看出，地震持续时间随地震烈度增大而变大，随场地土变软而变大。这与文献[20]由美国及中国的强震记录得到的结论完全一致。谱强度因子随烈度增大而变大，但随场地土变软而减小。
谱强度因子之所以随场地土变软而减小，主要是由于没有考虑场地土对烈度的影响；另一原因就是S0受式（1.68）的约束。从国内外地震震害调查可以发现：①基岩上的建筑物普遍破坏较轻；②软弱地基上的建筑物普遍破坏较重，这主要是由于地基失效造成的。因此，前苏联的抗震规范采用了提高烈度的方法来考虑软弱地基上建筑物破坏较重这一现象，而其他很多国家（包括中国）都是通过反应谱来考虑场地土对结构破坏的影响。由于本文采用基本烈度，对软弱地基既没有通过提高烈度的途径，又没有通过反应谱的途径来考虑其震害较重这一现象，而得到的结果是软土上的谱强度太小；另外，从可靠性分析来看，谱强度的影响远较持时为大。因此，为偏于安全且符合实际震害结果，建议谱强度因子均取表1.16 中数据第四列的结果。
2.地震加速度由白噪声通过线性滤波器平稳输出
由式（1.52）表示的地震动加速度过程知，A（t）还可以通过如下滤波方程的平稳解求得
或写成状态方程的形式
因此，地震动加速度A（t）可以由白噪声通过线性滤波器的平稳输出来确定，这将给结构的随机地震反应（尤其是非线性反应）分析带来很大的方便。
在地震动加速度模型的谱密度表达式（1.52）中，卓越频率ωg和阻尼比ξg 可以按不同的场地土类别确定其具体值。
因此，对于平稳地震动模型式 （1.52），待确定的参数只有两个：S0和Ts。S0是直接与地震动强度有关的参数，它将根据地震动的统计峰值来确定；Ts是平稳地震动持时，鉴于目前基于相对持时定义的90%能量强震持时Td的统计结果较多，它也与平稳持时的概念接近，故建议直接取平稳持时为90%能量的强震持时，即
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
