坝址（厂址）基岩运动的加速度、周期和持续时间优化

一些地震工程学者用实际观测到的地震资料进行统计分析，求得一些经验公式，借以推算坝址（厂址）的基岩运动最大加速度、卓越周期和地震持续时间。这些公式只适用于基岩面地震运动，不适用于一般地面地震运动。因为基岩面以上的土层性质悬殊，对地震波的传播、吸收、反射极不一致，故地面运动与震级之间缺乏有规律的相关关系。因此，近来都用基岩面运动加速度时程曲线进行建筑物的动力分析。把建筑物及其地基土层一起划分单元，成为一个抗震结构系统。把地震加速度作用在土层底 （基岩面），进行有限单元法计算。离坝址（厂址）近的震中虽然使坝址（厂址）发生较大的基岩运动加速度，但与较远震中相比，却不一定使坝址建筑物产生最大动力反应。因为动力反应的大小，不但与加速度大小有关，而且还与加速度的振动周期和地震历时有关。所以应当用远震和近震得到的坝址（厂址）加速度时程曲线分别作动力分析以资比较。因此，可选择离坝址（厂址）近的震中和震级大的远震震中推算坝址（厂址）的加速度时程曲线。

（1）坝址（厂址）基岩运动最大加速度可用古登堡 （B.Gutenberg）和里克特 （C.F.Richter）公式计算。先用式 （1.42）计算震中的基岩运动最大加速度，再用式（1.43）计算坝址（厂址）的基岩运动最大加速度。

式中 a0——震中基岩运动最大加速度，m/s2；

M——震级。

式中 a——坝址（厂址）基岩运动最大加速度，m/s2；

Fa——随震中距的增大而减小的衰减系数，可由图1.31 曲线查取，此曲线为古登堡和里克特提出的经验曲线。

衰减系数也可用勃罗姆（J.A.Blume）公式（1.44）计算，该式考虑了震中距和震源深两个因素。

式中 D——震中距；

h——震源深，与震中距的单位相同。

震中距、震源深的意义见1.3 节及图1.7。

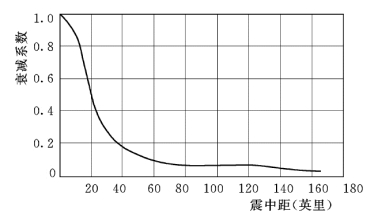
图1.31　衰减系数和震中距关系曲线

如果坝址 （厂址）到发震断层的垂直距离（即断层距，见图1.7）较近，而离震中较远，则坝址 （厂址）基岩运动最大加速度应根据断层距D1计算。什那贝尔（Schnabel）和西特 （H.B.Seed）建议的基岩上最大加速度与震级、断层距 （或震中距）的关系曲线如图1.32 （a）所示。后来，西特综合各家的成果，建议的关系曲线如图1.32 （b）所示。此曲线只适用于震源深度为10～15km。

古登堡里克特贝尼奥夫 （Benioff）也提出了基岩运动最大加速度与断层距的关系式，此式考虑了基岩运动卓越周期的影响，即

式中 F′a——衰减系数，用式（1.46）计算。

式中 D1——断层距，英里；

y0——常数，取48 英里；(www.xing528.com)

Tp——断层附近地震运动加速度的卓越周期，s，卓越周期的意义在下面说明。

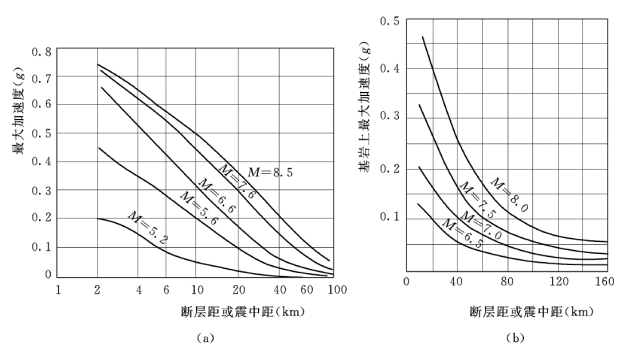
图1.32　基岩上最大加速度与震级、断层距 （或震中距）关系曲线

（a）什那贝尔和西特 （1973）建议的关系曲线；（b）西特建议的关系曲线

（2）坝址（厂址）地震运动的卓越周期。地震加速度（或速度、或位移）时程曲线上每秒时间内波峰的数目（指波峰谷在零线上下的波）为频率f，单位赫兹（Hz）。由于地震加速度（或速度、或位移）是随机函数，频率（或周期）不是常数。所以常用卓越周期来表征地震加速度时程曲线的周期性质。

卓越周期有几种定义：①对上述时程曲线用傅立叶 （Fourier）积分求得各谐波分量幅值和频率 （或周期）间的关系称频谱或傅氏谱，其主要谐波分量的周期称卓越周期；②反应谱上最大反应所对应的周期称卓越周期；③近似地将时程曲线上最大脉冲的周期称卓越周期，工程实用常按此定义。

根据观测资料统计，地震加速度卓越周期在各类不同地基上分别为：岩基0.1～0.2s，坚硬土层0.3～0.7s，软弱土层大于0.7s。

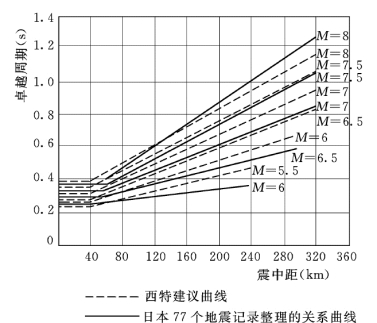
图1.33　卓越周期和震中距的关系曲线

古登堡和里克特根据实测资料分析，提出了震级为6 级时卓越周期和震中距的关系，费古罗阿（Figueroa）提出了震级大于7 级的卓越周期和震中距的关系。西特汇总整理了这些资料，提出了卓越周期和震中距的关系曲线，见图1.33 （文献[11]）中的虚线。日本根据14个坝址77 个地震记录得到的卓越周期与震中距的关系曲线，见图1.33 中的实线。

渡边给出了卓越周期和震级的如下关系式，可供参考。

式 （1.47）适用于震中距小于200km。

（3）地震持续时间。地震持续时间一般是指显著震动的历时，即超过某加速度限值的第一个至最后一个峰值之间的时间（s），常以超过0.03g 的历时为持续时间。

豪斯纳（1959）给出不同震级的地震在断层附近强烈震动的持续时间，见表1.13（见文献[12]）。

表1.13　断层附近强烈震动的持续时间

在表1.13 所列时间以外，还有一个延续相当长时间的衰减震动。此外，在离开断层较远处，持续时间还要长一些。

除表1.13 以外，在震中附近加速度超过0.03g 的持续时间，还可用下式计算

式中 td——持续时间，s。