表面面波的产生与传播特性及计算方法

面波是沿地球表面传播的弹性波，是体波经弹性模量不同的地层分界面多次反射、折射到达地球表面的波。面波有瑞利波和勒夫波，它们沿不同介质层的边界传播。

1.瑞利波 （即R波）

瑞利波是各向同性的半无限弹性体表面附近的波动。在地球表面为均质地层——没有特殊的表面层的情况下，沿地球的自由表面传播的波就是瑞利波。介质质点在前进方向的竖直平面内作后退的椭圆振动（当波向右传播时，椭圆是逆时针方向旋转），其长轴沿竖直方向。位移振幅随着深度的增大而逐渐减小。到极大深度，位移为零，如图1.18 所示。

沿弹性模量相差不太显著的两种弹性介质层的边界，或者其中一层为液体 （如在海底）亦可传播瑞利波。这种波称为斯东莱（Stonely）波。

图1.18 表示波的传播方向沿着x 轴，质点位移则在xz 平面内。瑞利波也可认为是P波和SV波的组合。

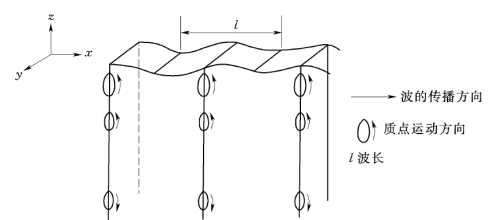
图1.18　瑞利波示意图

当泊松比μ＝0.25 时，x 方向和z 方向的位移为

式中 a——振幅参数，与振源状态有关；

k——波长（l）的参数，k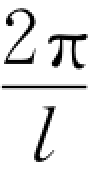＝，l 与振源状态有关；

vR——瑞利波速。

在弹性介质的表面，当μ＝0.25 时，质点运动椭圆的长轴为0.62a，短轴为0.42a。瑞利波的传播速度比剪切波稍慢，其比值R 可由下列方程式解得

2.勒夫波 （即L波）

当半无限弹性体的上面有均匀厚度的另一种弹性体表层，而表层的剪切波速度小于下层的剪切波速度时，则在表层及两层交界面附近存在勒夫波。勒夫波是这种地层中的SH波。

介质质点的振动方向平行于地表平面，与波的传播方向垂直，如图1.19 所示。图上abcd 为地表平面上的波动曲线，be 和cf 为质点位移沿着深度的分布曲线。勒夫波的传播速度可用下式计算

(www.xing528.com)

式中 vL——勒夫波速；

vs1、vs2——上层和下层的剪切波速；

G1、G2——上层和下层的剪切弹性模量；

H——上层的厚度。

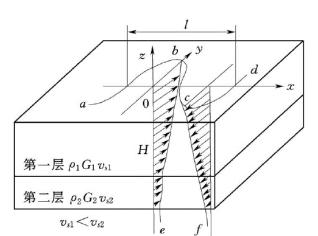
图1.19　勒夫波示意图

如前所述，面波是由震源附近的P波和S波，经不同地层的分界面反射和折射到达地球表层而形成的波。在震中附近，不产生面波。面波只能在距震中一定距离以外的地面产生。

P波和S 波产生的面波与震中的距离，可分别用式（1.24）和式（1.25）计算。

式中 Sp——P波产生的面波与震中的距离；

Ss——S波产生的面波与震中的距离；

h——震源深度；

vR——瑞利波传播速度；

vp——纵波传播速度；

vs——横波传播速度。

当μ＝0.22，瑞利波产生的范围为距震中0.65h （由P波产生）以外，或2.25h （由S波产生）以外的地面。