1.纵波 （即初波、膨胀波、P 波）
纵波介质质点呈压缩与扩张位移振动，质点位移的振动方向与波的传播方向一致，这种波亦称压缩波（compressional wave）、膨胀波（dilational wave）或疏密波。
为了说明纵波传播的机理，先考察等截面直杆内均匀压力波或拉力波传播的情况。图1.12 所示一直杆左端a 受一打击力，产生压应力σ。此压应力以速度vp向右传播，经时间t 由a 传播到b，传播距离为vpt，即ab 的长度。此时ab 段为压缩区。在时间t 以后的小时段Δt 内，压缩区从b 扩展到c，bc 的长度为vpΔt，这一段杆的压缩量为
这个值也就是ab 段在Δt 时段内向右位移的值，故ab 段质点的位移速度
为
图1.12 直杆纵波传播示意图
在时段Δt 内，脱离体bc 受到的冲量为
式中 A——杆的截面积。
脱离体bc 在Δt 之前位移速度为零；而在Δt 之后，位移速度为u·。故在Δt 时段内的动量为
由于I ＝M，得纵波传播速度为
式中 E——压缩弹性模量；
ρ——介质的质量密度。
拉力波速度的推导同上，其计算公式也与式（1.6）相同，不过E 为拉伸弹性模量。
图1.13 直杆质点位移运动示意图
或
这个方程式的一般解答是由 （x—vpt）或 （x ＋vpt）组成的任意函数 （有二阶导数的）。因此可取
常见的波形是正弦波或余弦波，即
式中 A——振幅，注意式（1.4）、式 （1.5）、图1.13 中的A 为面积；
l——波长；
vp——纵波波速。
(https://www.xing528.com)
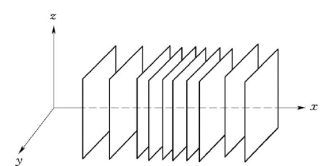
图1.14 无限弹性介质中的竖平面纵波示意图
地震纵波是均匀的无限弹性介质中传播的波，可按平面波考虑，如图1.14 所示。波的传播方向沿着x 轴，质点位移方向与波的传播方向相同。在垂直于x 轴的平面上，所有质点的位移都是同步的。即在同一个平面上，波的相位相同。由于振动，使原来间距相等的许多平面形成时疏时密的间距，这就构成纵波的传播。
用类似图1.13 的方法，对无限弹性介质切取脱离体。作用于脱离体的诸力与该图相同。因此可同样写出动力平衡方程式
由于脱离体的周围是无限弹性介质，其应力应变关系遵循广义虎克定律
式中 μ——介质的泊松比。
代入上式，得到
此微分方程式的解与式（1.10）～式 （1.12）相同，不过波速为
2.横波 （即次波、剪切波、S波）
横波介质质点呈现剪切位移振动，如图1.15 所示。质点位移的振动方向与波的传播方向垂直。介质只有畸变而无体积变化。这种波亦称剪切波 （shear wave）、切变波、畸变波。剪切波又可分为SH 波和SV波。介质呈水平剪切振动的波为SH 波，呈竖直剪切振动的波为SV波。
图1.15 无限弹性介质中的剪切波示意图
图1.16 微元剪切面上力的平衡图
式中 G——剪切弹性模量；
ρ——介质的质量密度；
w——z 方向（竖向）的位移；
——z 方向的位移加速度。
上式可写成
式 （1.19）的解与式（1.10）～式 （1.12）相同，不过，其中vp换成vs。横波不能在液体中传播，因为液体没有抗剪强度，其G 等于零。测定的饱和土的剪切波速，只代表土的性质。另外，水与土骨架相比是相对不可压缩的，故饱和土的纵波速度只代表水的性质。
图1.17 体波在地球内不同深度的传播速度
P波与S波的波速之比
体波在地球内的传播速度随深度增加而加快，如图1.17 所示。P 波、S 波在一些介质中的传播速度见表1.2。
表1.2 各种介质内的波速
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
