基于改进PCA的再制造过程质量异常识别方法

再制造过程不同于传统的制造过程，其过程更加复杂多变，过程中各种不确定性因素会随机发生，对再制造过程的产品质量产生很大的影响。所以，在再制造过程中如何快速识别、如何在小样本条件下，实现再制造过程的质量异常识别，对再制造过程非常重要。

传统的质量异常识别方法已经很难再适用于此复杂的环境，其研究的焦点也越来越多地集中在智能识别器上。如何在众多的智能识别方法中选择一种合适的方法对再制造过程质量控制显得特别重要。而主元分析法作为智能识别的一种典型代表，且在制造过程质量异常识别中得到了广泛的应用。主元分析法是以系统变量的样本序列所构成的系统数据矩阵为基础，通过建立少数的综合变量，实现了高维复杂数据的降维。该方法既可以做到保留原始变量中的重要信息，又能有效地实现系统中重要信息和噪声的分离。基于此，针对再制造小样本的问题与主元分析法自身需要大样本的限制，提出了基于改进PCA的方法，通过将求解协方差的方法转换成求解特征子空间矩阵来消除小样本的限制。基于改进PCA的废旧产品再制造过程质量异常识别方法的具体识别流程如图6-3所示。

1.传统的PCA理论

对于多变量的系统，用n维数据描述如式（6-16）表示：

X=[x（1），x（2），…，x（m）] （6-16）

式中：x（t）=[x₁（t），x₂（t），…，x_n（t）]^T（t=1，2，…，m）表示x的第t次采样值；n表示再制造系统变量个数；m表示质量样本个数。

随机矩阵X∈Rⁿ×m的协方差矩阵∑_X如式（6-17）表示：

通过求解下式

（λ_i-∑_X）B_i=0，i=1，2，…，n （6-18）

求得矩阵∑_X的特征值λ_i和特征矩阵B_i=[B_i1，B_i2，…，B_in]，且有

为了便于描述再制造过程质量数据，假定n个特征值满足λ₁≥λ₂≥…≥λ_n，同时可得随机矩阵M=B^TX。此外，由于矩阵B是正交矩阵，所以求解X的统计特征就可以转化成求解M的统计特征。

为了求得随机矩阵的最优变化量，与此同时弱化噪声对PCA的影响，选取前s个主元来代表数据中的主要变化，分解后以式（6-20）表示：

图6-3 再制造过程质量异常识别流程图

式中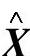：表示主元模型；E表示建模误差，一般为系统噪声。

从式（6-20）可以看出，只有提供稳健的协方差矩阵时，才能求得矩阵X的特征值与特征矢量。但是当数据样本较少时，是无法获得稳健的协方差矩阵的，继而会影响再制造系统过程质量异常识别。

从主元分析法的几何意义可以看出，该方法的实质就是将原坐标进行平移或者旋转，使更新得到的坐标原点与原数据样本群重心重合。设随机矩阵的分布

N（E（X），∑_X），在以E（X）为中心的超椭球上，X的密度是常数，以式（6-21）表示：

（X-E（X））∑_X^-1（X-E（X））^T=C² （6-21）

此时超椭球的各轴分别为

由式（6-22）

求得式（6-23）：

假设λ₁，λ₂，…，λ_n从大到小排列，那么超椭球上主轴沿着B₁的方向，即为PA1的方向，其余为较次要因素，依次为B₂，B₃，…，B_n。主元分析法的几何意义可以用图6-4表示。

从图6-4中可以看出，不同数据的坐标系的空间分布是不同，其旋转角度也是不相同的，这就说明不同的质量异常类型的数据空间分布及旋转的角度都是不同的，其对应的特征子空间也是不相同，所以可以通过不同的特征子空间来区别不同的质量异常类型，进而对异常类别进行识别。

图6-4 PCA的几何意义

假设再制造系统单独变量出现异常，共有p种异常类型，第j种异常模式记为f_j（j=1，2，…，p），每种异常模式对应的特征子空间矩阵为。

2.基于改进PCA的再制造过程质量异常识别

从主元分析法中式（6-20）中的由系统噪声引起的建模误差E满足高斯分布，因此可以得到在条件B和M下X的概率密度函数以式（6-24）表示：

因为随机矩阵M满足统一的先验分布，即π（M）∝1，所以由式（6-24）得到式（6-25），即得到在条件B下X的概率密度函数：

由式（6-25）得出，X的概率密度此时主要受映射矩阵W=BB^T的影响，假设该矩阵W满足冯·米塞斯-费舍尔分布^[30]。

由于矩阵B是正交矩阵，可以对其进行CS分解贝叶斯，具体模型^[31]以式（6-26）表示：

式中：V₁和Z为s×s正交矩阵，V₂为（n-s）×s半正交矩阵（V₂^TV₂=I_S）

C=diag{cosθ₁，cosθ₂，…，cosθ_s} （6-27）

S=diag{sinθ₁，sinθ₂，…，sinθ_s} （6-28）

式中，θ_i为主元坐标与空间基坐标之间主元的角度。空间基坐标为。

由式（6-26）～式（6-28）可以看出，各主元与基坐标之间的角度决定特征子空间矩阵B所在的空间位置，这点恰恰符合主元分析法的几何意义。(www.xing528.com)

将CS分解贝叶斯空间思想概念引入主元分析法中，将式（6-26）代入式（6-25）得到式（6-29）：

矩阵X可以分解成X=[X^T₁X₂^T]^T，由式（6-25）可以得到式（6-30）：

由式（6-24）～式（6-30）可以求得V₁、V₁和θ的后验概率分布函数以式（6-31）表示：

式中，θ=[θ₁，θ₂，…，θ_s]；σ可由信噪比求得，即。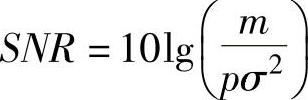

此外，V₁、V₁和θ的边缘概率分布可以由式（6-31）求得，分别以式（6-32）～式（6-34）表示：

式（6-32）、式（6-33）满足冯·米塞斯-费舍尔分布^[30]。式（6-34）中：θ_max

表示主元与基坐标的所有夹角的最大值；α_i表示；βi表示；γ_i表示。式（6-34）不属于目前已知的任何分布，很难

求得，所以，需要将其转化为已知的分布，设χ_i=sin²θ_i，χ=[χ_i]，将式（6-34）转化为式（6-35）：

其中，χ_max=sin²θ_max。此时的式（6-35）类似于贝塔分布：

此时，c_i和d_i分别取^[32]

c_i=0.5+0.25max{0，β_i}-0.25min{0，α_i-γ_i}

d_i=0.5+0.25max{0，β_i}+0.25min{0，α_i-γ_i}

式（6-35）能很好地取得近似值。

基于上述的算法与推理过程，通过下述方法实现随机抽样所得的特征子空间矩阵B（n）的计算。

输入：任意初始变量V₁^（0）、V₂^（0）、θ^（0）

1）for n=1，2，…，N_b+N_i。

2）根据式（6-32），通过吉布斯采样获得V₁^（n）。

3）根据式（6-33），通过吉布斯采样获得V₂^（n）。

4）通过吉布斯采样获得角度θ^（n）。

5）for i=1，2，…，s。

6）在X_maxBata（c_i，d_i）中的值，令X_i^r（0）为初始值，设X_iⁿ=X_i^r（0）。

7）foru=1，2，…，q。

8）从χ_maxBata（c_i，d_i）中获得χ_i^r（u）。

9）当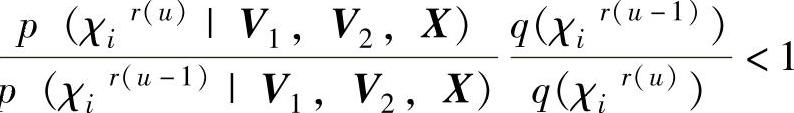

时，χiⁿ=χ^r_i^（u），其概率分布

以式（6-35）表示。

10）endfor。

11）。

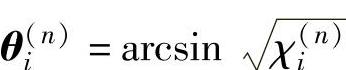12）endfor。

13）endfor。

输出：计算得出一组随机矩阵。

由上述的矩阵B^（n）可以估计出特征子空间矩阵以式（6-36）表示：

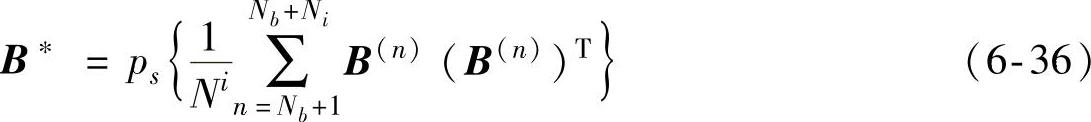
式中，p_s表示s个主元向量。

为了实现再制造过程质量异常的识别，采用特征子空间矩阵的相似性对异常类型进行识别，矩阵相似度函数以式（6-37）表示：

其中，ζ_u表示加权系数，代表不同方向主元的重要性，且∑^s_u=1ζ_u=1，1＞ζ₁＞ζ₂＞…＞ζ_u，相似度函数表示两个矩阵在s个投影方向夹角余弦值的加权和。因为ζ_u＜1，所以0＜d_j≤1。所得值越接近1，说明两个矩阵相似度越好。

根据再制造过程先验概率信息，以及上述的计算步骤，在再制造小样本条件下，运用CS分解贝叶斯方法估计其特征子空间矩阵。考虑不同类型数据对应不同的特征子空间矩阵，所以再制造过程中不同的质量异常数据分别对应不同的特征子空间矩阵。因此，可以通过比较数据与已知质量异常类型的特征子空间矩阵的相似度函数来确定质量异常类型，进而实现异常源识别。