构建面向动态多元非正态分布的再制造过程质量EWMA控制图

在实际的再制造过程中很难准确了解漂移的大小，直接人为设定光滑参数会带来较大的误差，降低监控的准确性。为了减少这类人为误差，同时加大监控过程漂移的范围^[16]，Capizzi和Massarotto^[17]在前人的基础上，提出了变化光滑参数的（Adaptive）自适应EWMA控制图（AEWMA），此控制图对过程发生的不同大小漂移都有效。

AEWMA控制图的再制造过程质量统计量定义以式（6-6）表示：

x_t=x_t-1+φ（e_t） （6-6）

式中，e_t=y_t-x_t-1，φ（e_t）表示“得分函数”。

若∣x_t-η₀∣＞H，系统发出报警信号，式中η₀为再制造过程目标均值，H为相对应的阈值。当y_t≠x_t-1时，式（6-6）可变形为式（6-7）：

x_t=（1-ω（e_t））x_t-1+ω（e_t）y_t （6-7）

式中，，这说明，再制造过程中权重是实时变化的。

在选取式（6-6）与式（6-7）中得分函数时，鉴于传统控制图及移动加权平均控制图各自的特点与优势，需考虑如下因素：

因素1：φ（e）是e的非降函数。

因素2：φ（e）=-φ（-e），即φ（e）是奇函数。

因素3：当∣e∣较小时，φ（e）≈λe0≤λ≤1。

因素4：当∣e∣较大时，φ（e）≈e。

综合上述四点因素考虑，给出以下三种得分函数：

式中，0≤λ≤1，k≥0，0≤p₀≤p₁，且p₀、p₁都为常数，并满足：。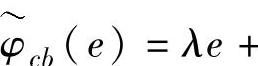

此控制图的参数包括光滑参数λ和控制限H。对于式（6-8）及式（6-9）中的得分函数，未知参数为三维矢量，设β=（λ，H，k），采用下述方法求解：

步骤1：确定要检测的漂移区间（μ₁，μ₂）及在控平均运行链长ARL，设为b。

步骤2：假定参数β^∗，使漂移为μ₂时，达到最小的ARL，即求解式（6-11）：

式中，ARL（μ，β）表示当漂移是μ，平均运行链长是ARL时，得到参数β。

步骤3：对于假定的α，设α=0.05，此控制图的最优参数β，即求解式（6-12）：

经计算得到参数β，满足当条件为漂移是μ₁时，取得最优的ARL；同时在漂移为μ₂的条件下，几乎取得最优的ARL。

为了使再制造加工过程质量监控更加精确，减少人为设定参数带来的误差，针对再制造过程发生的漂移大小不同的情况，利用实时变化的光滑参数实现再制造过程在线监控。鉴于式（6-8）函数的有效性及简便性，利用式（6-8）展开所提出的自适应方法。(www.xing528.com)

1.改进的再制造过程质量监控统计量

引入自适应的概念，将式（6-7）、式（6-8）带入式（6-3），得到新的再制造质量监控点的统计量如式（6-13）表示：

其中，

其中，v（e_i）=φ（e_i）/e_i1≤i≤t，。选择0≤λ≤1，k=3σ。

再制造监控统计量最终值T_t（ω，v（e_t））=maxT_jt²。

2.改进后的再制造过程质量监控控制限的确定

引入自适应的概念后，最终再制造质量控制动态控制限由式（6-5）变为式（6-14）：

使用的动态控制限需要特别强调，动态控制限是在线确定的，而不是在监控前确定的。即这些控制限与原始数据相关的，并没有做任何假设，这是构造与分布无关控制图的关键。

定理：在可控情况下，对于任何连续的F₀，当t≥1时，Pr（ARL=t）=α（1+α）^t-1

虽然T_t（ω，v（e_t））是条件与数据分布无关的，但要通过求解再制造加工质量统计量所有值，进而求得H_t（α）是很难实现的。此外，鉴于再制造控制限统计量公式本身及求解的复杂性，同样无法通过分析方法来解决H_t（α）的求解问题。因此，提出了一种算法近似H_t（α）。

推理：对于每一个j，T_jt（ω，λ）与T_jk（ω，v（e_t））无关，k≤t-ω。

依据此理论，将上述求解再制造过程控制限统计量公式（6-14）简化为

当t较大时，式（6-15）有助于求得H_t（α），因为概率只与窗宽ω内的T_i有关，而不是与再制造所有参数的T_i有关，因此，采用如下算法。

1）当t=1时，{-m₀+1，…，1}随机进行排序，假设某一排序为，设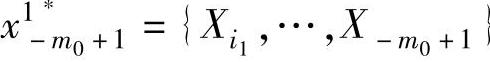，求得相应的T₁^∗（ω，v（e_t））。循环该排序过程b次，最后通过求解T₁^∗（ω，v（e_t））所有值的（1-α）经验分位数，得到相应的条件阈值H₁（α）。

2）当t＞1时，假设初始值i=0。按照上述随机排序方法，计算求得再制造统计量T_k^∗（ω，v（e_t））max（1，t-ω+1）≤k＜t，。若T_k^∗（ω，v（e_t））＜H_k（α），求得一个T_t^∗（ω，v（e_t）），进入下一次排序，且i=i+1；反之，舍弃该排序。循环该过程，当i=b时停止。随后通过求解T_t^∗（ω，v（e_t））的（1-α）经验分位数，获得条件阈值H_t（α）。

3.再制造过程质量监控相关参数的选择

（1）m₀的选择 ADFEWMA是一种自启动控制图，从再制造开始阶段就利用动态控制限检测过程异常。因此，若m₀太小，不利于再制造过程质量的异常检测。因为控制图需通过获取适量多的观测值满足第一阶段的学习，用以保证再制造过程初始阶段的稳定性。通过实践证明，要保证控制图有稳健良好的表现，在再制造过程质量出现异常前，需要20～100个再制造历史观测数据（越多越好）。

（2）初始阶段 当t较小时，例如t＜w，再制造质量统计量里面包括历史观测值的排序。另外由于过程漂移通常是在过程正常运行一段时间后发生，所以此时t对再制造过程不会产生影响。若在较早的情况下，即t较小时，过程发生漂移，则需满足ω=max{5，min{ω₁，t}}，式中ω₁表示满足（1-λ）ω1≈0的窗宽。因此，求得ω=5。

（3）光滑参数λ的选择 对于最终控制图中光滑参数λ的确定，不仅要考虑其对于非正态分布的稳健性，同时还要考虑其在再制造过程中，对于不同漂移的监控的可靠性。在再制造过程正常运行情况下，无论权重如何选取，都是与过程数据分布无关的。因此，λ的选取方法与传统控制图参数λ的取值方法类似。针对不同的漂移，选择合适的λ值。所以，根据偏移量和再制造毛坯质量不定情况，选择λ∈[0.025，0.2]。