构建与分布无关的非参多元EWMA控制图

目前，废旧产品再制造系统存在许多不确定性，导致废旧毛坯的质量分布不确定，而有关不确定问题的研究大多集中在非参方法上。秩和检验作为非参方法的一种，不需要提前对样本做任何假设，即可应用于总体分布形式未知或分布类型不明数据的方法中，使得基于秩和检验所构建的非参多元EWMA控制图（Distribution-Free Exponentially Weighted Moving-Average，DFEWMA）具有能够很好地适应再制造过程系统不确定性的特点。而DFEWMA控制图的特点就在于其控制限是随时间变化的，并通过不断更新观测值进行实时改变，它不是在监控前预设的，而此控制图动态控制限的使用恰好符合再制造过程质量分布不确定的特点。由于消除过程数据维度及数据分布两者的限制，在不同情况下该控制图依然能获得特定可控平均运行链长。通过构造一系列非参数的再制造质量监控秩和检验统计量，保证了控制图是与数据分布无关的，这也是此控制图的核心思想。在统计量构造过程中，重点是如何使用条件概率，即控制图在当前时刻的统计量超过控制限，而在此之前，再制造过程并未出现过程异状，由此保证了控制图能够取得特定错误报警率。接下来，针对再制造过程质量分布不确定性特点及条件概率的使用，具体阐述了DFEWMA控制图统计量的构建过程，进而说明再制造过程质量具体的监控过程。

1.再制造过程质量监控统计量的构建

假设两个独立再制造样本{X₁，X₂，…，X_τ}与{X_τ，X_τ+1，…，X_t}，并且它们分别服从分布f（x；μ₀）和f（x；μ₁）。原假设为h₀：μ₀=μ₁，备择假设h₁：μ₀≠μ₁。

原假设h₀：μ₀=μ₁，等价于当j=1，2，…，p时，它们的每一个成分μ_j0≠μ_j1，因此，对于观测的再制造样本的每一个成分，利用Wilcoxon秩和检验^[14，15]，如式（6-1）表示：

式中，R_ji表示X_ji在再制造混合质量样本中的秩。

当μ_j0≠μ_j1，T_jt的值就会变大。随后合并再制造质量观测值的每一个成分T_jt，j=1，2，…，p，此过程采用“max”或“Σ”。采用T_t=maxT_jt²，当T_t值变大，超出设定界限时，拒绝h₀。在再制造过程中，虽然无法获得原始分布，但由于它依赖于变量与变量间的相关性，其条件与分布无关，所以当给定再制造质量数据样本时，能求得阈值。

假设有m₀个独立同分布（iid）的再制造过程历史观测值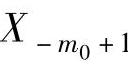，，…，X₀∈R^p，p≥1，第i个质量观测值是X_i=（X_1i，…，X_pi），多元位置变点模型以式（6-2）表示：

式中：τ为某一再制造质量异常变点；f₀表示再制造过程在控的分布函数；f₁表示失控时的分布函数，假设两函数都是连续的。(www.xing528.com)

在实际再制造过程中，f₀和f₁是否相同不确定，假设再制造过程位置参数μ0=（μ₁₀，μ₂₀，…，μ_p0）^T和μ₁=（μ₁₁，μ₂₁，…，μ_p1）^T是不同的。

定义再制造质量监控点为x^t_k，j=-（x_jk，…，x_jt）^T和x^t_k=（x^t_k，1，…，x^t_k，p）^T，此外选择一个窗宽ω和一个光滑参数λ。在每一个质量监控时间点，假设为t时刻，构造一个再制造质量监控点的统计量如式（6-3）表示：

式中：R_jti表示再制造监控点X_ji在样本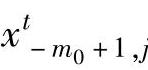中的秩；ω表示窗宽；λ表示光滑参数；m₀表示历史观测点数量；j表示再制造质量观测点的第j维参数。

T_jt（ω，λ）用来检验两个再制造质量监控样本点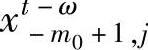和x^t_t-ω+1，j中观测值的位置参数是否相等。观测点离得越近，权重越大；反之，权重越小，且权重符合指数分布，并以此函数形式衰减。当变点τ的第j个监控成分中某一个位置参数变动，当t＞τ时，质量监控最终值T_jt变大，若超出特定值，引发报警。

2.再制造过程质量监控控制限的确定

利用与分布无关的控制图实现再制造加工过程的质量监控，关键在于再制造质量监控的控制限的确定，使得条件概率为一特定的常数，且此之前过程并没有出现异常，发出报警。通过式（6-5）确定监控点的控制限：

式中，α表示错误报警概率。