基于可拓发散树与TRIZ的再制造设计冲突消解方法优化

1.再制造设计冲突消解框架

根据上述设计冲突消解方法综述，在充分考虑了不同方法之间的优势与局限后，我们提出了基于可拓发散树与TRIZ的再制造冲突消解框架，如图4-14所示。

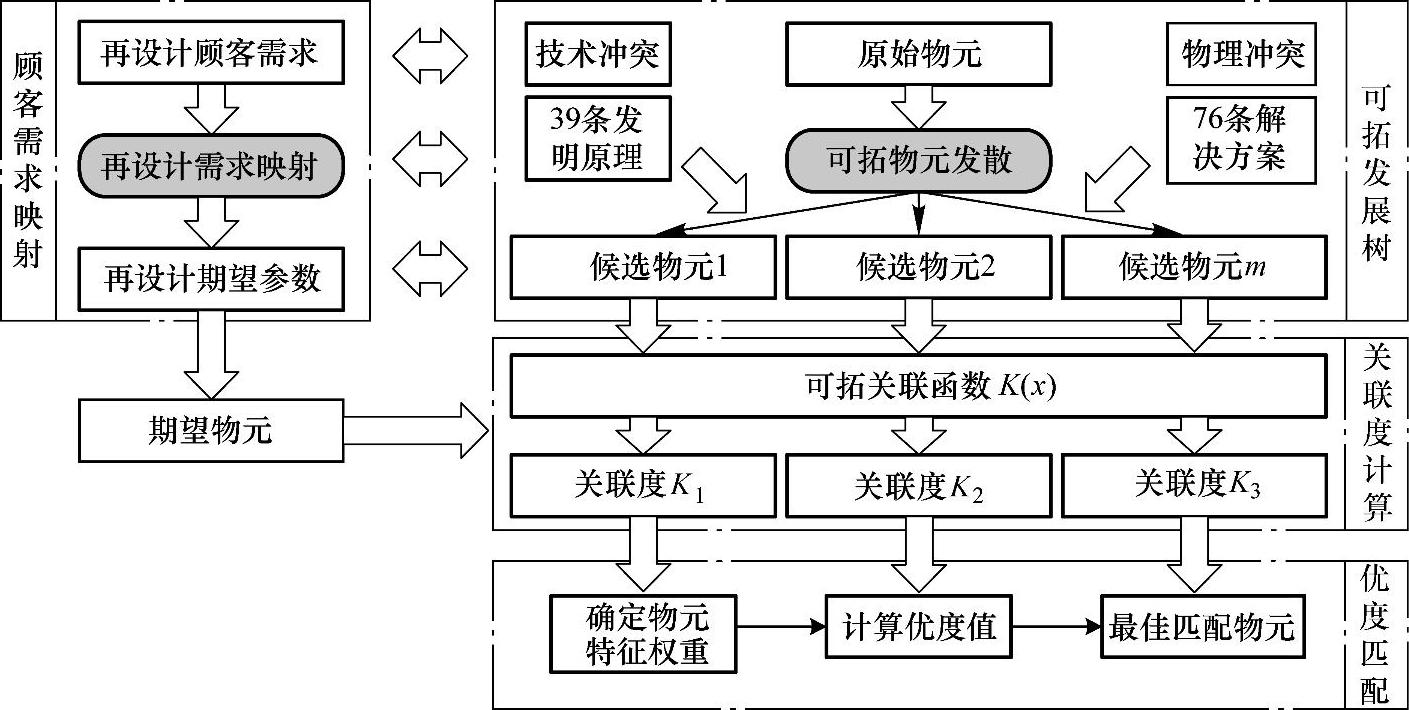
图4-14 基于可拓发散树与TRIZ的再制造冲突消解框架

该框架将TRIZ理论与可拓理论相结合，以4.2.4得到的最大化满足用户需求的再制造设计质量参数为基础，通过对可能产生冲突的再制造设计质量参数进行分析，并将其对应结构形式化表示为结构物元。通过分析再制造设计冲突的类型，即若为技术冲突，则提取产生冲突的元素，并通过TRIZ矛盾矩阵得到相应的创新原理；若为物理冲突，则通过物质-场模型选取适当的解决方案。在此基础上，根据得到的TRIZ创新原理，对形式化的废旧机电产品结构物元进行可拓变换与物元发散，最终得到若干候选物元。通过可拓关联函数，分别计算各个候选物元与期望物元之间的关联度，并通过可拓优度评价决策出最佳匹配物元作为再制造设计方案的参考。

2.废旧机电产品结构物元的构建与变换

为了达到综合性能提升与充足的市场竞争力，需要对废旧机电产品的特定结构进行重新规划。为了降低原废旧机电产品结构、功能及材料等方面对再制造设计带来的限制，宜采用一种标准化集成的方法。可拓学通过形式化的模型分析事物拓展的可能性及创新性规律，有益于创新性设计方法的规范化与流程化。形式化的废旧机电产品结构物元可表示为

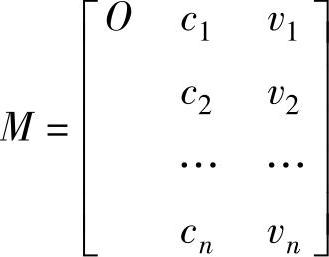
其中，O为需要进行创新性设计的废旧机电产品结构，特征矢量C=（c₁，c₂，…，c_n）为结构O对应的相关特征；特征值矢量V=（v₁，v₂，…，v_n）为每个特征对应的定量值或定性值。

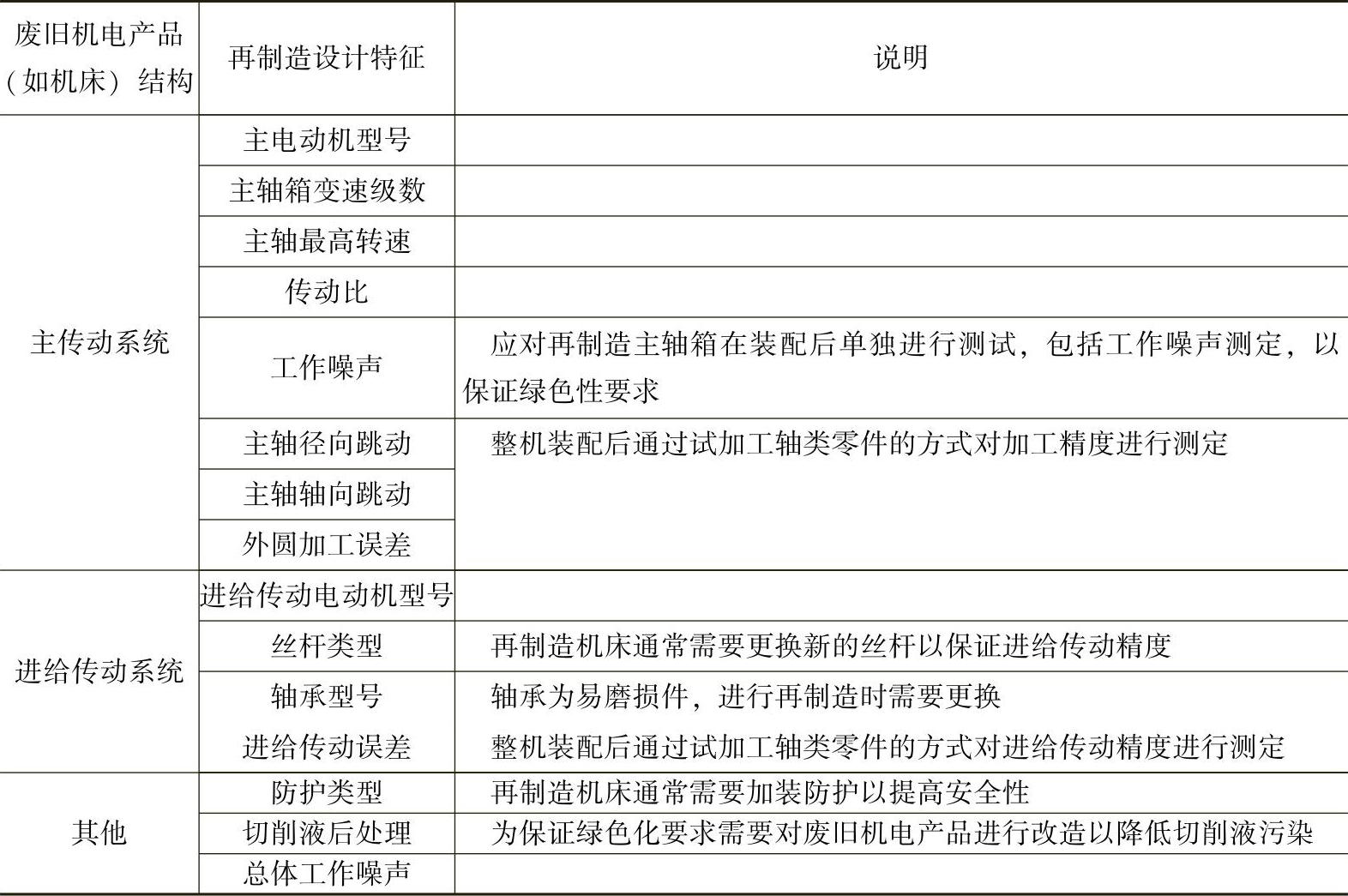
在对废旧机电产品特定结构进行形式化过程中，需要选取其与特定结构相关的特征。根据废旧机电产品再制造实践，通常需要对废旧机电产品（如机床）的主传动系统、进给系统等进行改进，其典型再制造冲突特征见表4-6。

表4-6 典型再制造冲突特征

一个物元可以通过可拓变换得到出多个非空物元集合，即

M=（O，C，V）┤{（O，C₁，V₁），（O，C₂，V₂），…，（O，C_m，V_m）}则废旧机电产品结构物元可拓展出m个物元，这些拓展出的物元与原物元具有相同的物元特征及不同的特征量值。此外，还可以拓展出具有相同特征量值的物元集合，即

M=（O，C，V）┤{（O，C₁，V），（O，C₂，V），…，（O，C_m，V）}

或者相同特征的物元，即

M=（O，C，V）┤{（O₁，C，V₁），（O₂，C，V₂），…，（O_m，C，V_m）}

或者在不同参数下同一对象关于同一特征具有多个取值的物元^[80]：

M（t）=（O（t），C，V（t））┤{（O（t₁），C，V₁（t₁）），（O（t₂），C，V₂（t₂）），…，（O（t_m），C，V_m（t_m））}

在实际解决问题的过程中，往往需要多种拓展方式相结合，这便形成可拓发散树。通过可拓发散树可以找出废旧机电产品特定结构的若干拓展方式，为创新性设计提供解决思路。然而，可拓发散树只能提供物元拓展的方向，且更注重于方法的推演，与工程实际结合的并不紧密^[81]。因此，我们将TRIZ与可拓学相结合，通过TRIZ中的创新原理作为可拓发散的发散方向。基于TRIZ的可拓发散方法流程如图4-15所示。

对再制造设计期望物元特征值而言，每一个特征的最优点可能是该域的中值，也可能不是中值，例如对于精度特征来说其期望值往往越小越好。因此，定义期望物元域左侧距为

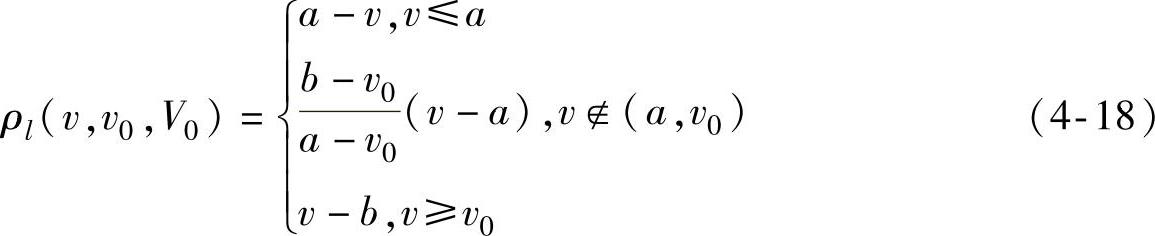
式中，V₀为期望特征值域，V₀∈[a，b]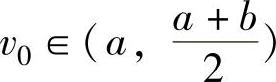，，为V₀的左侧最优值。当

v₀=a时，式（4-18）变为

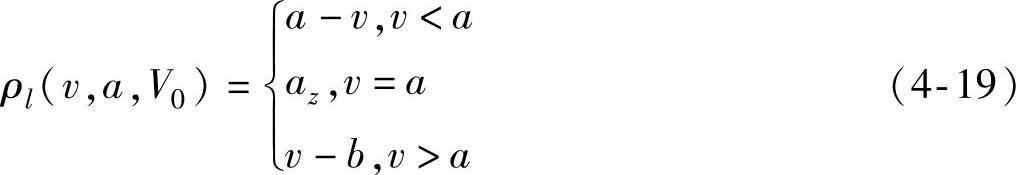
其中，

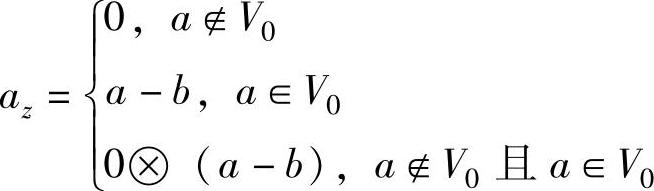
3.基于物元模型的关联函数

当通过基于可拓发散树与TRIZ的创新方法对废旧机电产品结构物元进行发散后会得到若干候选物元，为了识别出与期望物元最为接近的候选物元，要对候选物元与期望物元之间的相似关系进行分析。对于期望物元，其特征值V通常为区间值（域），而可拓关联函数是研究点与域相关关系的有效工具，为此定义如下概念。

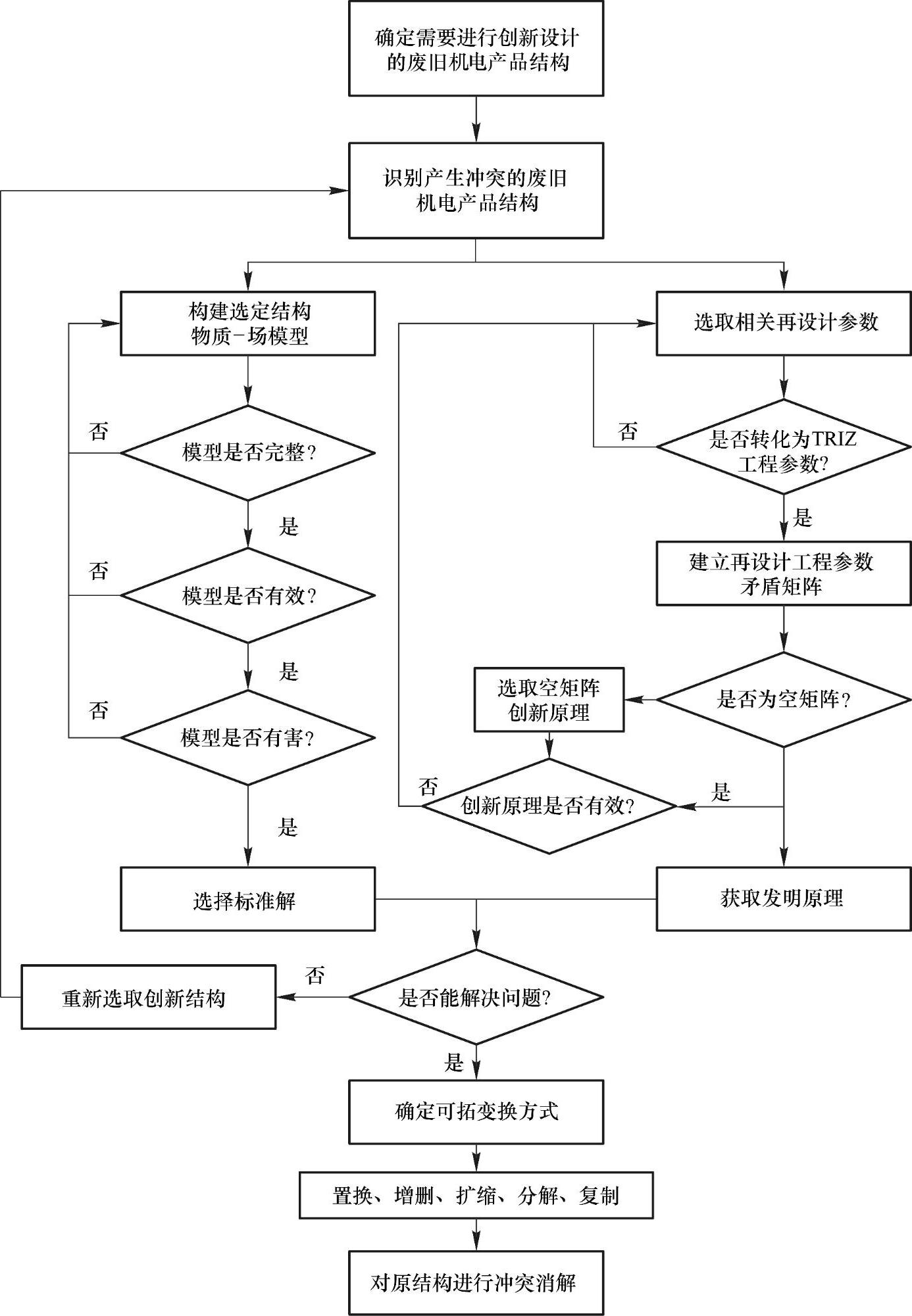
图4-15 基于TRIZ的可拓发散方法流程

（1）侧距 同理可定义期望物元域右侧距为

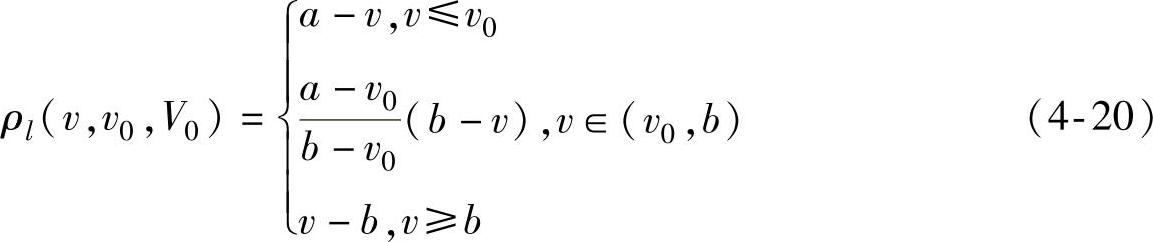
当x₀=b时，(www.xing528.com)

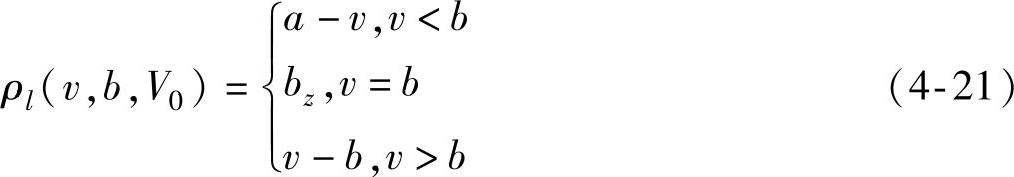
其中，

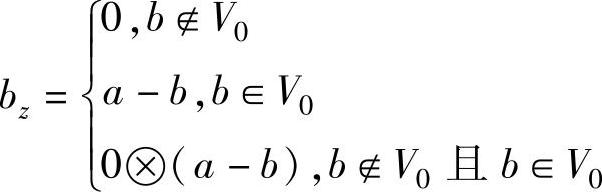
（2）位值 在废旧机电产品冲突消解中，还需考虑候选物元特征值与期望特征值域之间的关系，因此，定义位值为

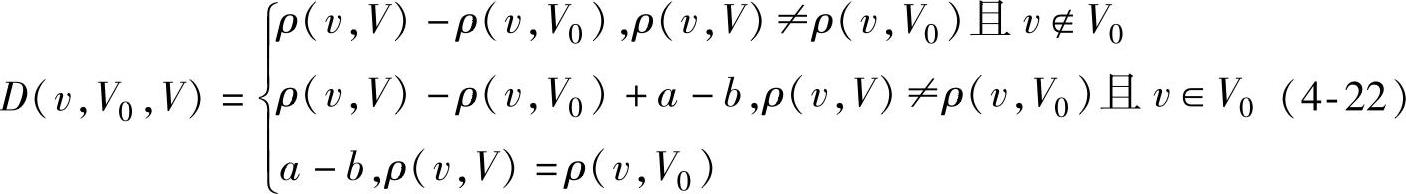
式中，ρ（v，V）为候选物元特征值v与可行特征值域V的侧距，V∈（c，d）且V₀∈V。

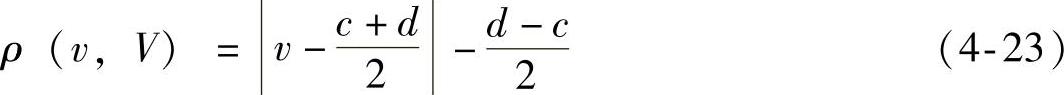
（3）关联函数 在得到物元特征值与期望特征值域的位值及侧距后，由可拓关联函数表征两者之间的关联度为

4.基于可拓优度评价的再制造冲突消解决策

通过可拓优度法可对某个废旧机电产品结构物元的优劣进行定量分析，具体步骤如下。

（1）选取衡量指标 在对某一物元进行评价时，首先要从待评价物元确定评价特征，即衡量指标。例如对于期望物元M_e，其存在n个物元特征，可从中选取s个衡量指标，且s≤n，则衡量指标集为

S=（s₁，s₂，…，s_s）

衡量指标的选取应保证所选取的指标具备目标相关性、全面性、可行性与稳定性，以保证评价结果之有效性。

（2）确定衡量指标权重 衡量指标以权重表征其重要程度。为了降低人为主观评价对决策结果的影响，可采用层次分析等方法确定指标权重，从而确定衡量指标权重集为

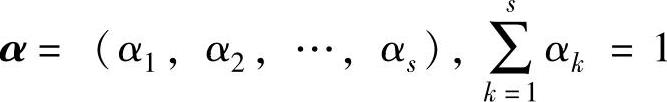
（3）计算规范关联度 在计算候选物元特征与期望物元特征之间的关联度时，若对应的衡量指标为定性指标或离散指标，则其关联度为

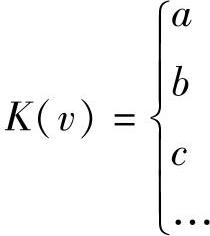
即对期望物元的衡量指标s_k对应的期望指标值V₀进行分级，每级评分可由专家通过资料进行评定。

若为连续的定量指标，则关联度计算方法由4.3.3确定。若第k个衡量指标与第i个候选物元对应特征值的关联度为K_k（v）i，则每个候选物元对应第k个衡量指标的关联度向量为

K_k=[Kk（v）₁，Kk（v）₂，…，Kk（v）_m]

k∈[1，s]

由式（4-25）对关联度进行规范化：

k∈[1，s]，i∈[1，m]

即可得规范化关联度矢量为

K_k^∗=[K_k1，K_k2，…，K_km]，K∈[1，s]

（4）计算优度值 由向量K_k可知，对于第i个候选物元，其每一特征关于衡量指标s的规范关联度向量为

K_G=[K_1i，K₂i，…K_si]^T

i∈[1，m]

则第i个候选物元的优度值为

通过优度评价，可选择优度最大的候选物元作为与期望物元最佳匹配的物元，并以此作为再制造设计方案的参考依据。