再制造设计质量参数分析与优化

以沈阳精新再制造有限公司的废旧CAK6136机床再制造过程为例，对其进行再制造设计质量参数规划。CAK6136主要用于轴类、盘类零件的精加工与半精加工，在机械制造领域应用广泛。通过市场对当前销售的再制造CAK6136机床的反馈情况来看，用户不仅希望再制造机床仅达到性能的恢复，更希望达到性能的提升；然而，当前该厂的再制造机床往往无法达到期望的市场竞争力。因此需要对现有再制造方案进行改进，并结合顾客调研结果总结出顾客需求，主要为希望提高精车外圆与端面的能力及提高加工较长工件的能力。通过企业技术部门的分析及当前的再制造机床出厂标准，确定其相关的再制造设计质量参数，见表4-1。

表4-1 相关的再制造设计质量参数

由表4-1可知，项目1、项目2、项目3及项目5均由两项参数组成，而项目4包括一项参数。通过当前的市场反馈情况来看目前出厂标准显然已不能满足用户需求。为了提高再制造机床的市场竞争力，需要制定更加严格的出厂标准，同时还需要保证再制造成本不会出现大幅提高的情况。现以变量x₁表示项目1中的a参数，以x₂表示项目1中的b参数，以此类推，至x₉表示项目5的b参数。从该厂已经售出的6台再制造机床的反馈情况可以掌握这6台机床的不同参数与用户满意度之间的关系。已售出的这6台再制造机床相应于表4-1的再制造设计质量参数及其相应的用户满意度，可通过质量屋的形式体现，如图4-5所示。

图4-5 再制造设计质量屋

其中，用户需求为分解的4条由技术语言表述的决策目标，且每台再制造机床的再制造设计质量参数均为出厂实测值，其对应的用户满意度评价以1～10为基准，即10为最大化评价值。

将质量屋中的数据代入式（4-11）中可以得到用户需求与再制造设计质量参数之间的相关关系，如主轴端部的几何精度与主轴轴向窜动与主轴轴肩支撑面跳动之间的模糊非线性回归方程为（h=0.5）

minZ=36a²₀+0.045²a²₁+0.105²a²₂+0.01（a²₃+a²₄+a²₅）

0.5a₀+0.003a₁+0.008a₂+c₀+0.006c₁+0.016c₂≥9.6

0.5a₀+0.003a₁+0.008a₂-c₀-0.006c₁-0.016c₂≥-9.6

0.5a₀+0.0035a₁+0.0075a₂+c₀+0.007c₁+0.015c₂≥8.6

0.5a₀+0.0035a₁+0.0075a₂-c₀-0.007c₁-0.015c₂≥-8.6

0.5a₀+0.004a₁+0.0085a₂+c₀+0.008c₁+0.017c₂≥7.6

0.5a₀+0.004a₁+0.0085a₂-c₀-0.008c₁-0.017c₂≥-7.6

0.5a₀+0.005a₁+0.009a₂+c₀+0.01c₁+0.018c₂≥6.3

0.5a₀+0.005a₁+0.009a₂-c₀-0.01c₁-0.018c₂≥-6.3

0.5a₀+0.003a₁+0.01a₂+c₀+0.006c₁+0.02c₂≥9.2

0.5a₀+0.003a₁+0.01a₂-c₀-0.006c₁-0.02c₂≥-9.2

0.5a₀+0.004a₁+0.0095a₂+c₀+0.008c₁+0.019c₂≥7.4

0.5a₀+0.004a₁+0.0095a₂-c₀-0.008c₁-0.019c₂≥-7.4

a₀，a₁，a₂≥0

解以上方程可得：a₀=1.047，a₁=148.8，a₂=58.103，c₀=8.3736，c₁=-15.006，c₂=-7.3944。

因此，主轴端部的几何精度与主轴轴向窜动与主轴轴肩支撑面跳动之间的模糊非线性关系表示为

y₁=（8.3736，1.047）+（-15.006，148.8）x₁+（-7.3944，58.103）x₂同理，可以得到其他用户需求与不同再制造设计质量参数之间的模糊关系及x₃与x₅、x₄与x₆之间的自相关关系，见表4-2。

此时，所有用户需求与不同再制造设计质量参数之间的模糊关系及不同再制造参数之间的自相关关系都已得到；若要得到改进后的再制造设计质量参数值，需要将上述模糊关系代入产品规划式（4-15）中，在此之前，还需对目标函数进行定义。一般来说，产品规划方程的目标函数均为使用户满意度最大化，因此，可构建出再制造机床的综合满意度与面向不同用户需求的用户满意度评价之间的函数关系。

若定义当用户满意度评价值为10时，综合满意度为1；而用户满意度评价值为1时，综合满意度为0，则两者之间的函数关系可归纳为如下线性关系为

式中：V为综合满意度；y为顾客满意度评价。(www.xing528.com)

若存在n个用户需求，需要有n个用户满意度评价与之相对应。在本例中存在4个用户需求，若将这4个用户需求按照权重进行分配，可得

式（4-17）即可作为产品规划方程的目标函数，将图4-5中每一台再制造机床针对每一项用户需求的用户满意度评价值代入式（4-12）可得这6台再制造机床的综合满意度，见表4-2。

而根据式（4-15）可得到如下约束：

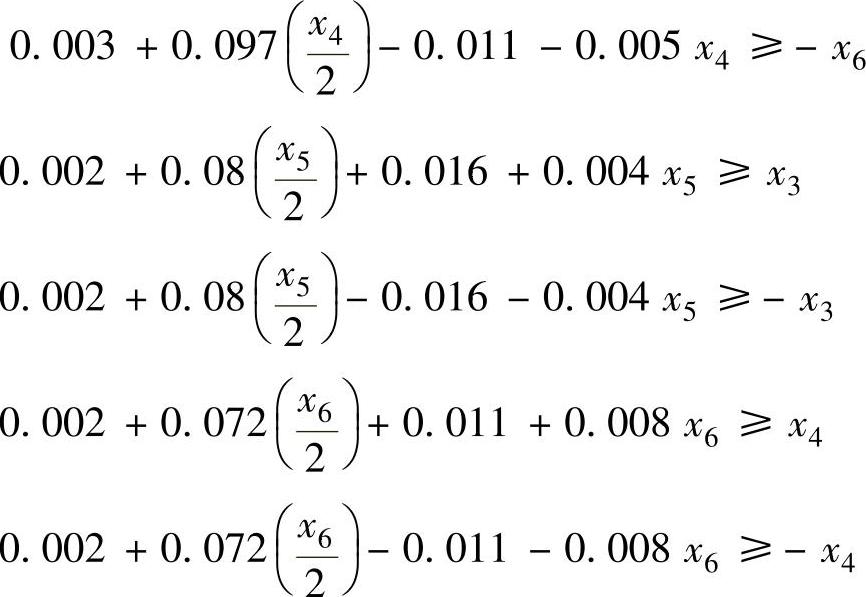
表4-2 再制造机床综合满意度

以上约束包括了用户需求与用户满意度评价之间的模糊关系约束，也包括了再制造设计质量参数x₃与x₅、x₄与x₆之间的自相关关系约束。此外，由于再制造综合性能提升并不意味着性能的无限提升，其中，还要考虑再制造性能提升的同时带来的再制造成本及方案可行性等因素的影响。因此，除了上述约束以外，针对每一个再制造设计质量参数还应限定一个性能提升的最大限度值，一般由企业内部根据企业实际情况，综合再制造成本进行制定，见表4-3。

在对废旧机电产品进行再制造性能提升时，针对每一项再制造设计质量参数的性能提升都不应超过表4-4中的给定值，否则会使在制造成本超过所能接受的范围。因此，式（3-17）、式（4-15）得到的所有约束与表4-4中的约束值共同组成了产品规划方程。

解此规划方程可得出所有的再制造设计质量参数值为：x₁=0.01mm，x₂=0.02mm，x₃=0.019mm，x₄=0.014mm，x₅=0.019mm，x₆=0.01mm，x₇=0.04mm，x₈=0.02mm，x₉=0.02mm，此时目标函数V=0.98。

和原再制造机床的出厂检测标准进行对比可以发现，主轴轴线对溜板移动的平行度在垂直面内的标准值由原来的0.02mm提升为0.019mm；在水平面内的标准值由原来的0.015mm提升为0.014mm。尾座套筒轴线对溜板移动的平行度在垂直面内的标准值由原来的0.02mm提升为0.019mm；在水平面内的标准值由原来的0.015mm提升为0.01mm。

表4-3 模糊关系表

表4-4 再制造设计质量参数限值

精车外圆时在纵横面内直径的一致性标准值由原来的0.03mm提升为0.02mm。经过改进后的综合满意度为0.98，均高于表4-3所示的现有的6台再制造机床。

此外，在建立再制造设计规划方程时，若按照传统的建立方法，即只考虑模糊关系中值的影响，根据式（4-13）可得如下约束为

8.37-15x₁-7.39x₂≥y₁

11.54-1.67x₃-5.26x₄-3.68x₅-329x₆≥y₂

9.55-27.6x₇≥y₃

9.07-6.06x₈-33.9x₉≥y₄

0.016+0.007x₃≥x₅

同样，以式（4-17）为目标函数，以表4-4中再制造设计质量参数为提高上限，以相同的方法可得出再制造设计质量参数为：x₁=0.005mm，x₂=0.01mm，x₃=0.016mm，x₄=0.011mm，x₅=0.016mm，x₆=0.011mm，x₇=0.025mm，x₈=0.015mm，x₉=0.02mm，V=0.81。将通过改进的规划方程得出的结果、通过传统规划方程得出的结果、与表4-4中的提升极限的差值结果对比汇总于表4-5。

表4-5 结果对比

从对比结果来看，x₁、x₂、x₅、x₇、x₈、x₉的值与表4-4中的性能提升极限值相等，而x₃与x₆均与极限值相差很小。尽管由传统规划方程得出的再制造设计质量参数，在性能提升方面要比由改进规划方程得出的再制造设计质量参数高，然而其最终满意度仅为0.81，明显低于构建的规划方程得出的用户满意度（0.98）。

实践表明：我们提出的基于非线性回归的再制造设计改进质量规划方程，不仅能够显著提高用户对再制造机床的满意度，还能有效缓解再制造性能提升与再制造成本之间的矛盾。