1.模糊回归方程
自从Zadeh[19]于1965年提出模糊数学的理论后，模糊数学在全世界范围内得到了快速发展，为处理具有不确定性的事物提供了有效的方法。随后Zadeh于1975年指出对于自然界普遍存在的模糊现象及系统，均可以用含有模糊系统参数的函数表示[20]。日本学者Hideo在此基础上，提出在回归分析中采用模糊线性函数对模糊现象进行表示并首次系统地建立了基于对称三角模糊数的模糊线性回归数学模型，以式（4-1）表示[21]：
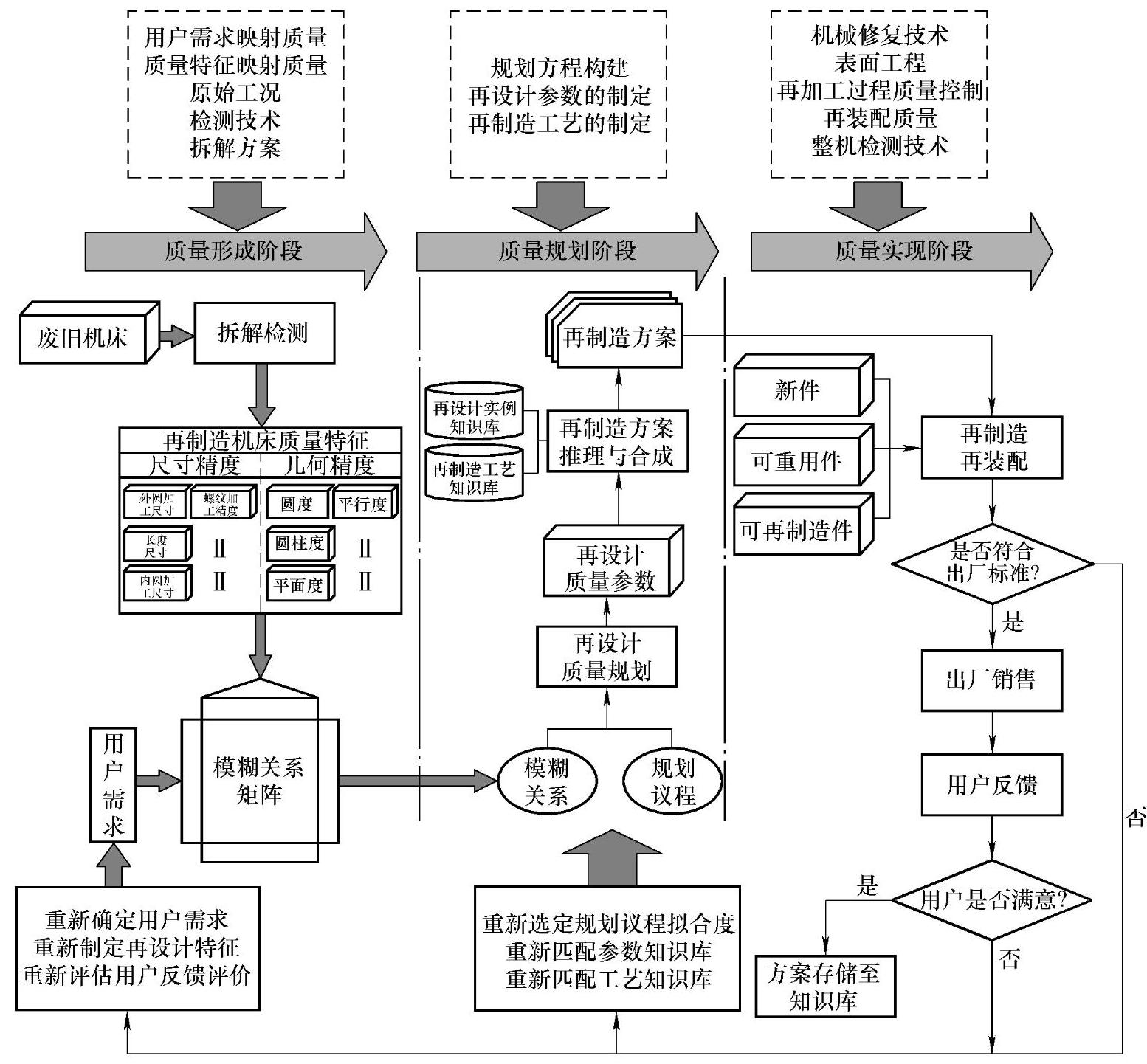
图4-2 基于模糊非线性回归和质量屋的再制造设计质量参数决策框架
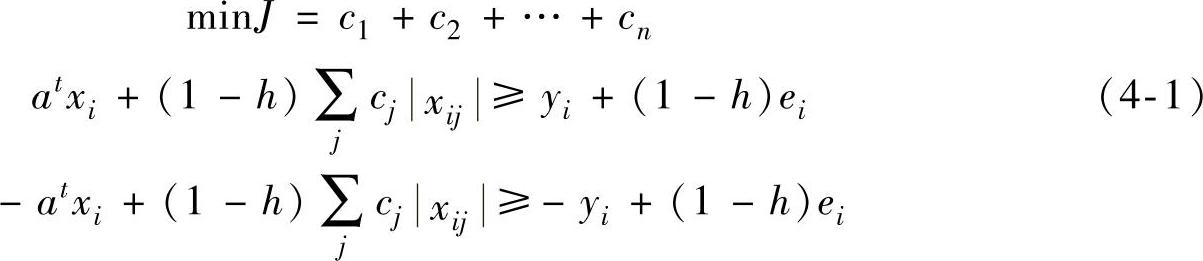
式中：at为三角模糊数的展值；ei为输出值yi的展值；xij为模糊特征值；h为拟合度，在后文中将进行讨论。
目前，线性模糊回归已在多个领域得到应用，例如Chung等[22]建立了基于模糊线性回归的评价基准模型；Poleshchuk等[23]提出了基于二型模糊集的回归模型；Al-Oth-man[24]基于线性模糊回归建立了电力经济性负载模型用于电力设施的选址优化。
近年来，还有学者将模糊回归方程与质量屋相结合用于工程参数的提取与优化。质量功能展开（QFD）是一种使用户满意度最大化的产品配置方法[25]，由日本质量专家水也滋和赤尾洋二提出后同样得到了迅速发展，并与其他多种方法进行整合取得了更好的效果[26]。Kwang-JaeK等[27]将模糊线性回归法引入QFD中用来确定用户需求及工程特性之间的相关关系及自相关关系；随后Fung等[28]则将模型中的非对称三角模糊数拓展为非对称梯形模糊数。同年，我国学者陈以增[29]首次提出采用模糊非线性回归法并应用到QFD中确定相关关系及自相关关系，以便能够更加真实地反应用户需求与工程特性之间的关系。
近年来，对模糊线性回归模型的研究主要集中于其拟合度的优化问题，如Liu等[30]讨论了在基于对称三角模糊数的线性回归方程中拟合度的选取问题；Liu等[31]将基于对称三角模糊数的线性回归方程与拟合度的优化选取进行了整合；Chen等[32]将拟合度的优化问题延伸到基于非对称三角模糊数的线性回归方程。
2.再制造设计质量参数决策
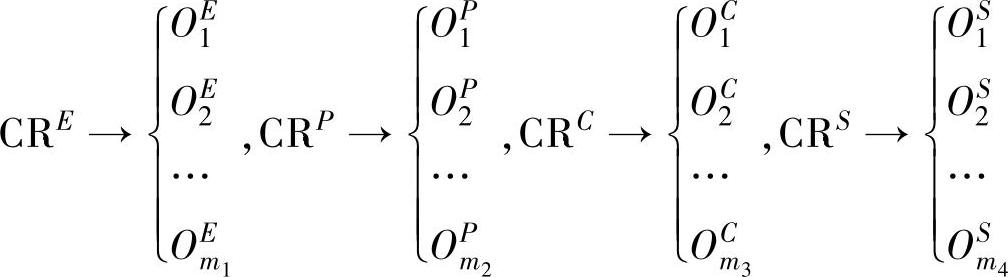
由于用户需求具有不确定性，为了保证从用户需求到再制造设计质量参数转化过程的准确性，在建立质量屋时需要将用户需求转化为决策目标，即加工效率转化为m1项决策目标，加工精度转化为m2项决策目标，再制造成本转化为m3项决策目标，绿色性转化为m4项决策目标，共有m项决策目标O，每项决策目标对应的权重为ωi，且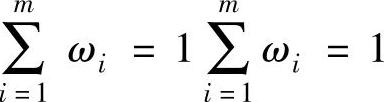
，其发散式转化过程为
对于多目标的决策问题，用户需求的模糊性导致用户需求与再制造设计质量参数之间的相关关系及不同再制造设计质量参数之间的自相关关系存在诸多不确定性，而模糊非线性回归法是模糊关系定量化处理及分析的有效工具，能够有效解决相关关系中的不确定性带来的影响。因此，提出采用模糊非线性回归法对用户需求与再制造设计质量参数之间的相关关系及不同再制造设计质量参数之间的自相关关系进行分析。根据模糊关系方程，设用户需求与再制造设计质量参数之间的相关关系为
式中，
为第i项决策目标的顾客满意度，共有m项决策目标。
设矢量xi=（xi1，xi2，…，xin）x1=（xi1，xi1，…，xin）为与决策目标
相关的n项再制造设计质量参数矢量，
为模糊关系矢量，若用对称三角模糊数A
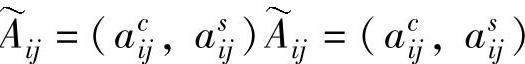表示模糊关系，则其隶属度由式（4-3）表示为
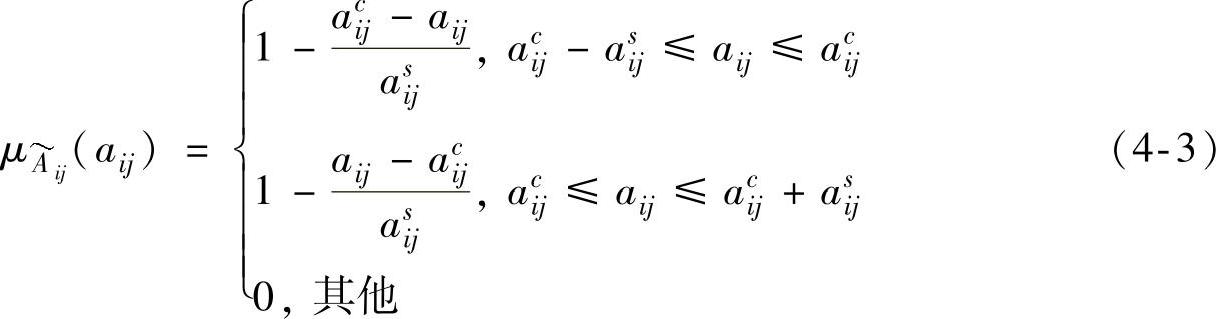
式中：acij为第i项决策目标中第j项再制造设计质量参数对应的模糊关系期望值，即中值；asij为波动值，即展值。
对于
，有
设aci=（aci1，aci2，…，acij，…，acin）T，asi=（asi1，asi2，…，asij，…，asin）T，xi=（xi1，xi2，…，xin）T，
则
则式（4-1）变为
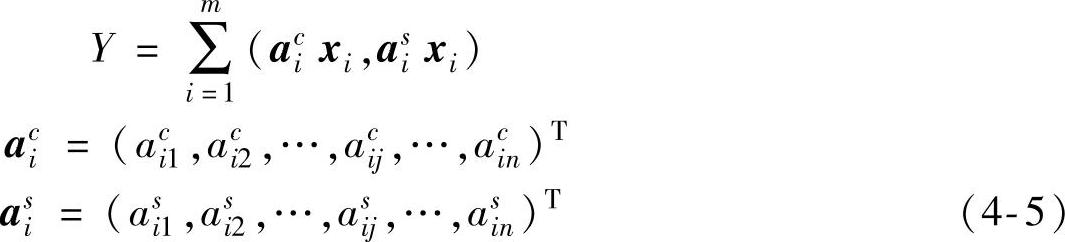
其隶属度函数为
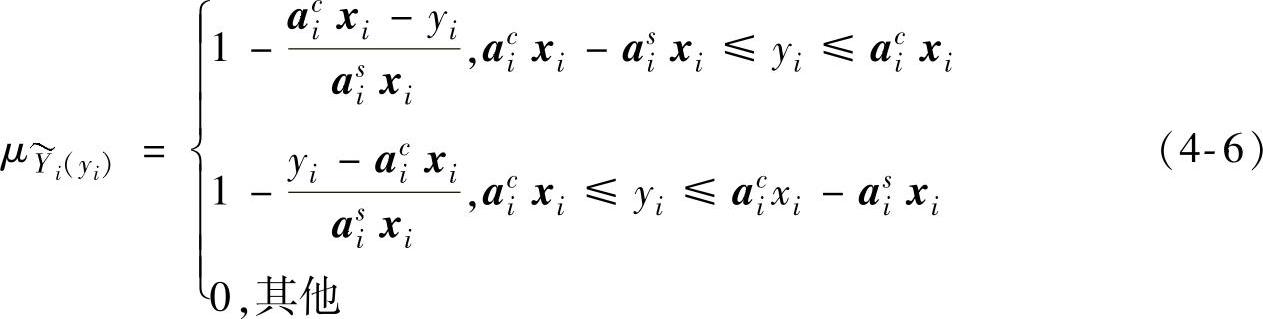
基于非线性模糊回归的用户需求与再制造设计质量参数关系分析，得出所有模糊关系的模糊输出为最小如图4-3所示。(www.xing528.com)
由图4-4可知：
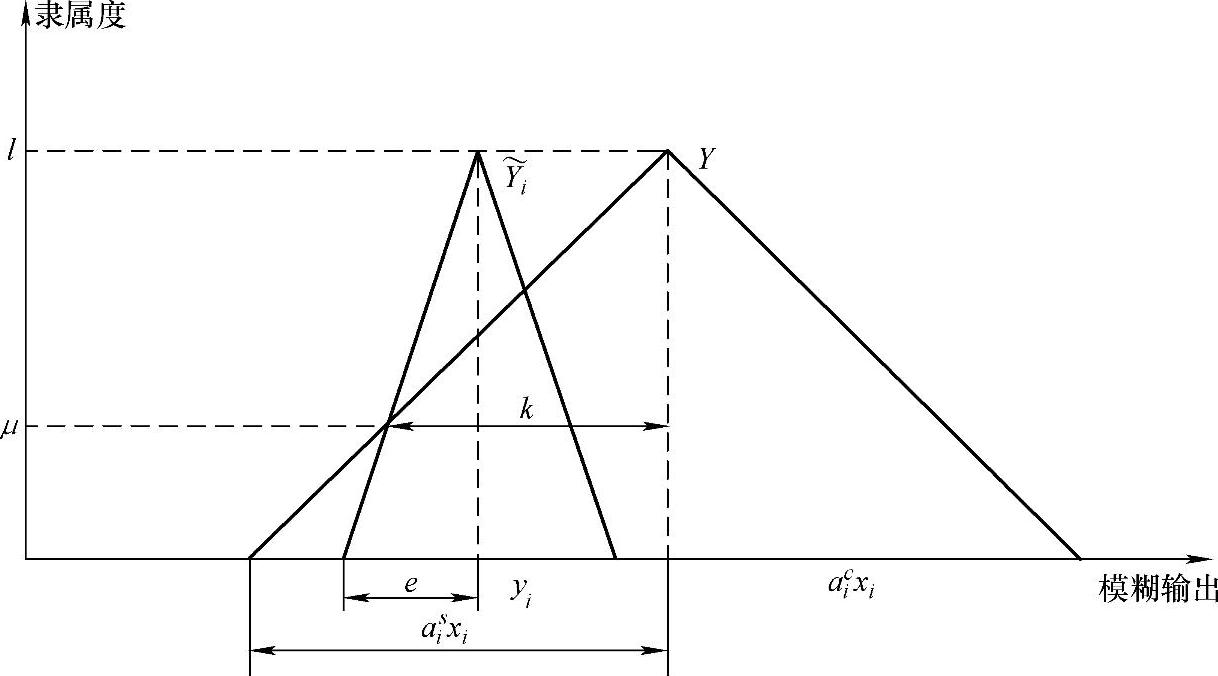
图4-3 模糊输出
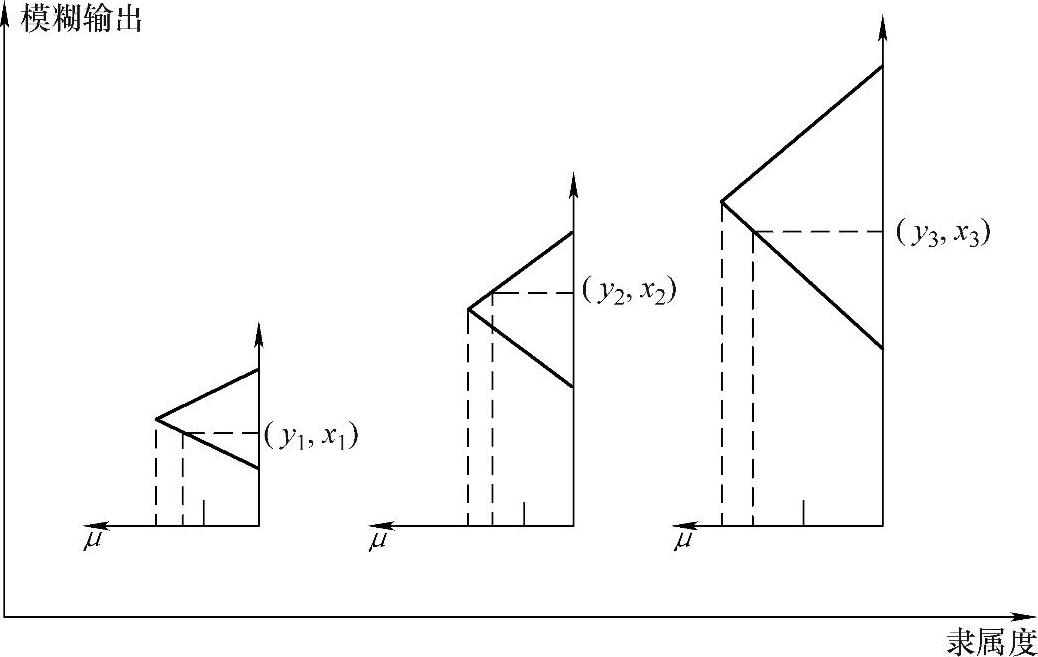
图4-4 隶属度
其中
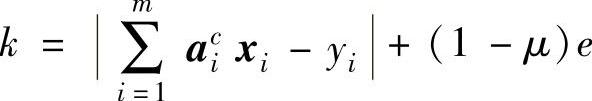
则
式中，μ即为隶属度，令μ≥h，则有
（1-h）asixi+acixi≥yi
（1-h）asixi-acixi≥-yi （4-9）
表示为式（4-10）：
式中，h∈（0，1）为拟合度，根据实际情况由决策人员主观确定，与样本数量相关。
将式（4-9）代入式（4-10），可得
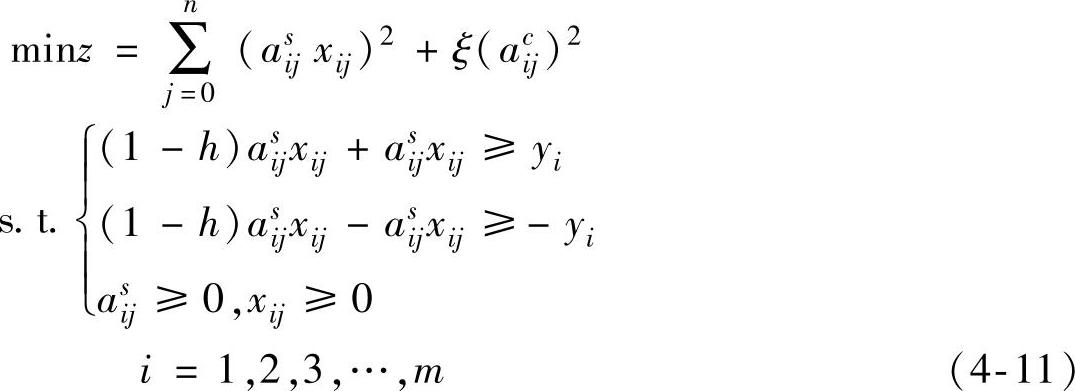
式中，ξ为一很小的正数。
通过式（4-11），可得第i项用户满意度yi与再制造设计质量参数xij之间的模糊
关系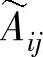
，同理可得不同再制造设计质量参数之间的自相关模糊关系，由式（4-12）
表示：
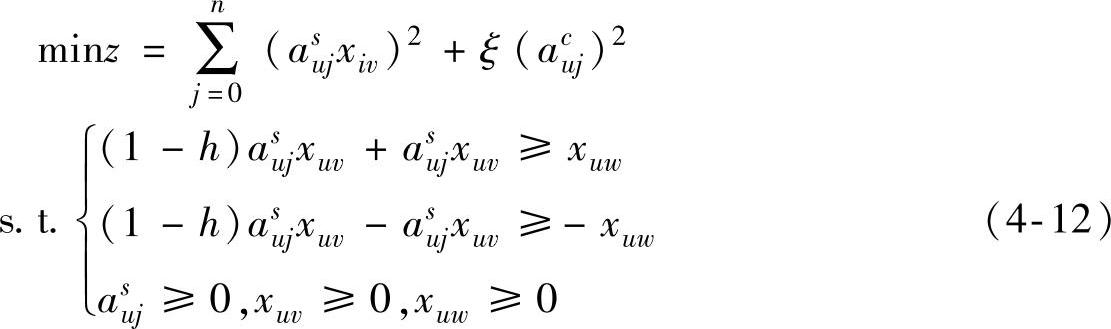
u=1，2，3，…，l
v，w∈1，2，…，n且v≠w
式中，xuv为在第u组自相关关系下，与xuw具有相关关系的再制造设计质量参数，共有l组自相关关系。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
