基于主S-N曲线的焊缝疲劳寿命预测方法

首先计算等效结构应力，取焊缝节点排序方向为横坐标，图11-7所示为

按照焊缝长度排列的等效结构应力，图中给出了最大等效结构应力出现的位置。然后将主S-N曲线向下取两个标准差，计算R=-1时对称循环载荷作用下的疲劳寿命。同样取焊缝节点排序方向为横坐标，图11-8给出了与焊缝位置对应的疲劳寿命计算结果，该疲劳寿命最短位置与最大等效结构应力位置一致，基于结构应力法计算得到的平均寿命为74400次，这一结果与由疲劳试验获得的平均寿命75000次几乎完全吻合，预测得到的最短寿命位置也与实际发生疲劳裂纹的位置完全一致。而在±2σ区间的疲劳寿命预测结果（12400～412000次）与12个疲劳试验样件的试验结果的循环次数（30000～200000次）也一致。

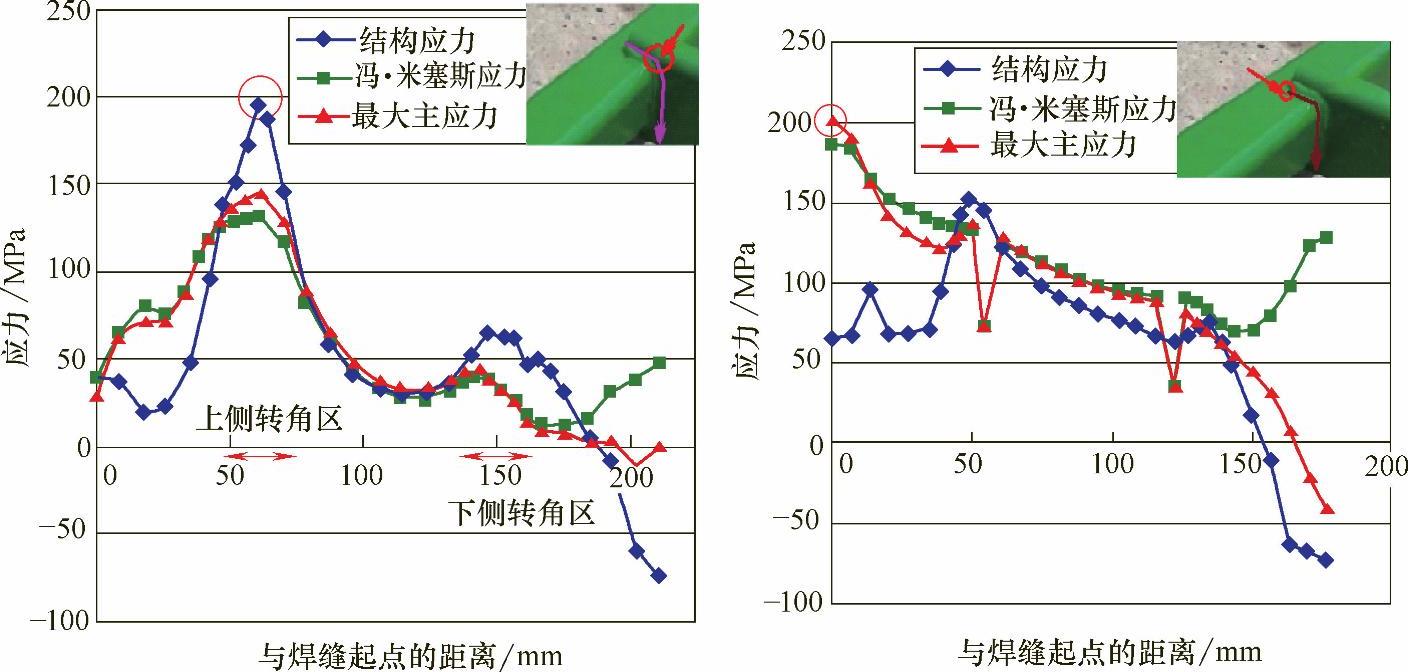
图11-5 计算得到的最大结构应力及最大主应力位置示意

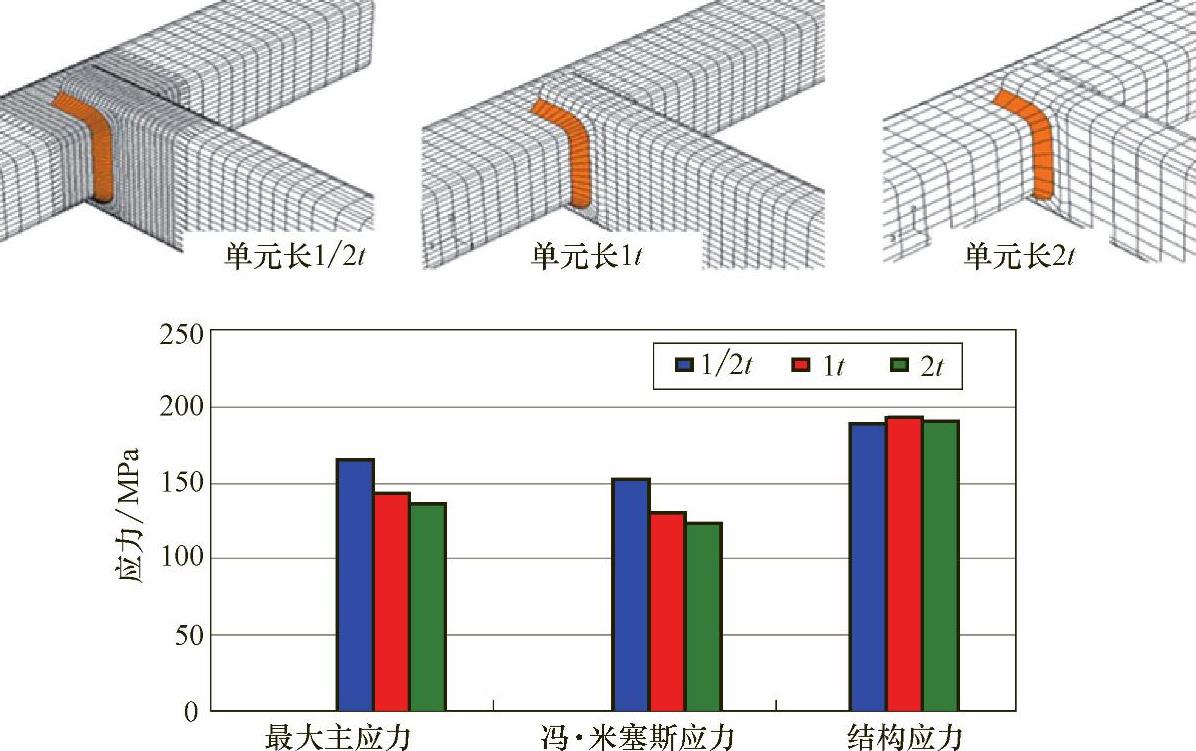
图11-6 三种不同有限元网格尺寸计算的三类应力结果对比

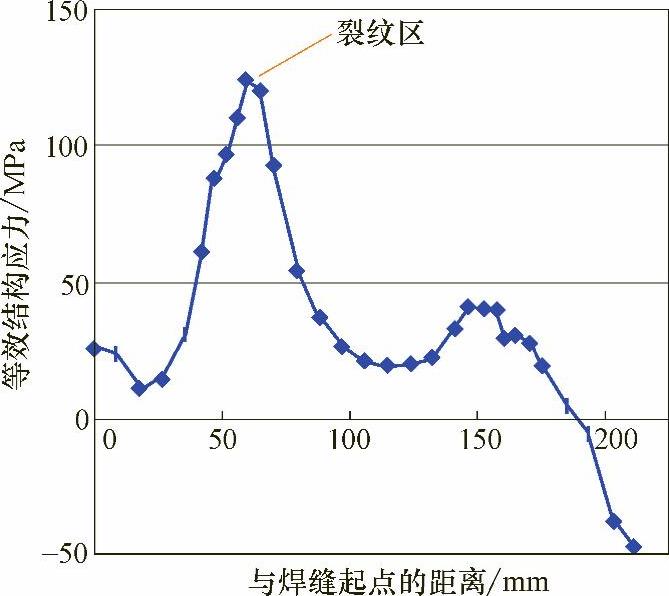
图11-7 焊缝长度方向上的等效结构应力(www.xing528.com)

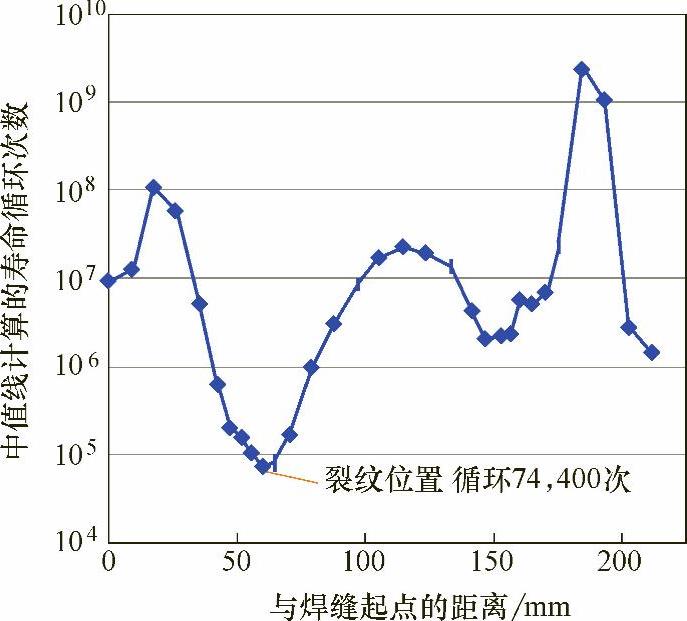
图11-8 焊缝长度方向上的疲劳寿命

在第一次“疲劳挑战”结束之后，为使“挑战”结果更让人信服，SAE的FD&E又组织了第二次“疲劳挑战”，这次疲劳载荷改为变幅载荷，而其余所有的测试样本等信息与第一次“疲劳挑战”的信息保持一致，但是焊缝端部焊脚尺寸增大很多，如图11-9所示。焊缝端部焊脚尺寸的增大，使得该处应力集中增大，结构应力的计算结果也是该处最大，省略第二次“挑战”计算过程的细节描述，基于结构应力法的第二次疲劳寿命预测结果与实测结果还是完全吻合。

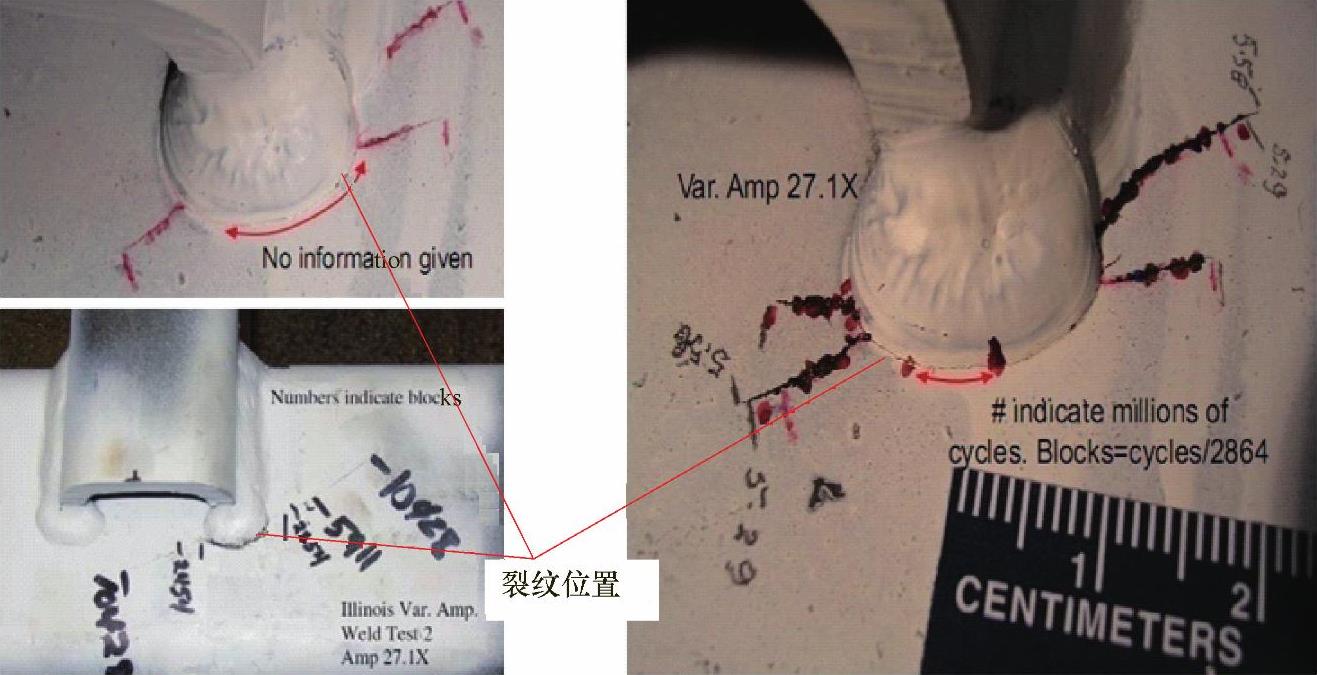
图11-9 焊缝端部焊脚尺寸增大以后的形状

上面的案例表明：将有限元计算得到的节点力转换为焊缝处的结构应力，其网格不敏感的力学特征得到了证明。两次“挑战”的盲评结果与实际情况的一致性，证明了结构应力法有能力给出焊缝处的应力集中。与参加“挑战”的传统方法比较，结构应力法的计算结果与试验值最接近，优势明显，因此得到了此次“挑战”的冠军。