应变法结构分析与低周疲劳机理详解

与经典板壳理论相一致，一个结构件通过弹性或弹塑性变形后，可以假定沿着厚度变形仍然维持在一个平面上，这个假定十分重要，它是以下公式中定义与计算伪弹性应力或应变的基础。

为了简单却不失一般性，考虑材料假定为各向同性，而且为完全弹塑性。如图10-15所示，有两种加载方式需要考虑：一是弯曲加载，弯曲将对板两面的塑性变形有贡献；二是膜载。图10-15给出了大于材料的屈服强度R_eL的弯曲应力σ_b与膜应力σ_m之和。

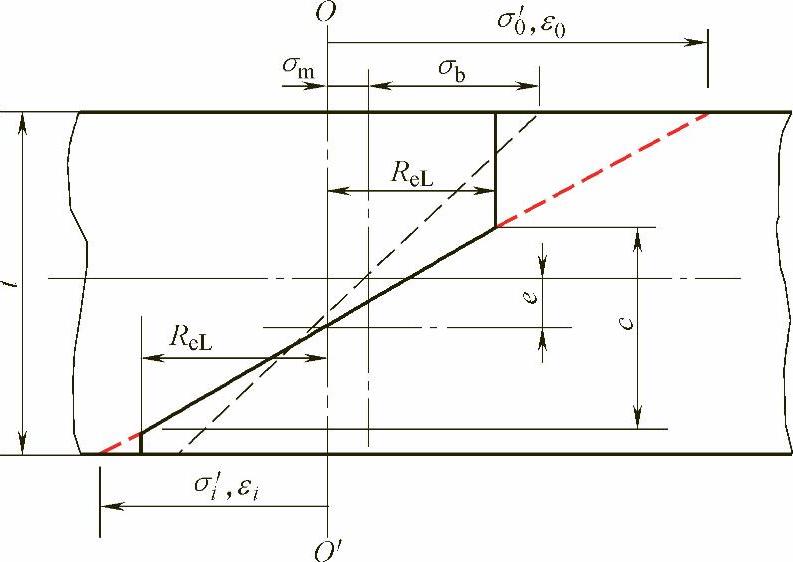
图10-15 弹塑性区间里的结构应变定义

（1）弯曲为主的加载 首先考虑弯曲载荷为主要载荷的低周疲劳，在这种情况下，对于贯穿厚度的一个假想切面上，如果使用弹性计算的方式，那么可以得到如图10-15中所示的σ_m和σ_b，这时，合并以后的应力显然已经超过材料的屈服强度R_eL，因此线弹性计算的名义应力必须被重新分配：一是满足平衡条件（力的平衡、力矩的平衡）；二是满足屈服准则（这里假定满足冯·米塞斯准则）。下面给出这两个重要参数的推导。

参考图10-15，为简单起见，假定完全弹塑性材料的屈服强度是R_eL，那么图中用粗线表示的应力分布必须满足平衡条件，即：

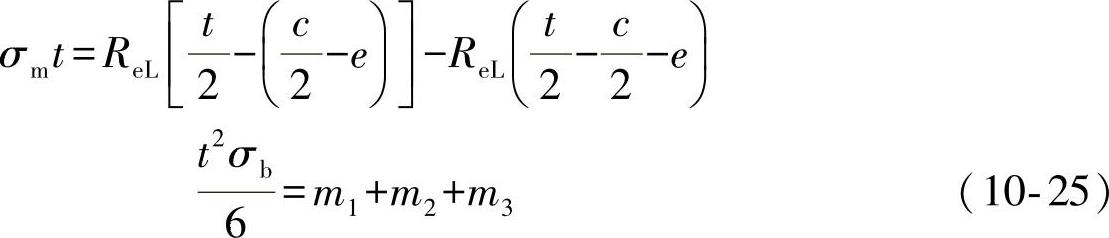
这里：

由于c＞0表示有非零的弹性芯，因此由式（10-25）力的平衡公式得到：

将式（10-26）代入式（10-25），这样就得到了计算弹性芯的公式（10-28）。

上述推导适用于线性硬化的材料或幂硬化材料，而弹性芯参数c与中性轴移位参数e的计算公式中含σ_m和σ_b，因此还需要数值手段才能获得这两个参数。

假如材料的屈服强度R_eL已知，根据板厚t、弯曲应力σ_b、膜应力σ_m，就可计算得到弹性芯参数c，它是产生塑性变形以后留下的弹性芯的大小。中性轴移位参数e是产生塑性变形以后中性轴的偏移量。

假如膜应力分量σ_m=0，且弹性芯c=0，那么式（10-28）就退化为经典的极限应力状态：σ_b=3R_eL/2，而弹性核非零的条件可以表述为

假设弹性核存在且占主导地位，那么它将控制厚度的变形行为，根据几何关系可以很容易地获得弯曲变形的曲率：

式中 R——弯曲的曲率半径。根据如图10-16所示的变形关系，可以推导出受弯曲载荷以后板的最外层纤维和最内层的纤维结构应变，推导过程如下。

图10-16 最外层纤维和最内层的纤维结构应变

类似于参考文献[15][16]中关于低周循环疲劳试验的伪弹性标称应力的伪弹性结构应力的做法，将式（10-31）计算得到的应变乘以材料的杨氏模量，就可以得到仅有名义牵拉应力情况下的伪结构应力的两个分量：(www.xing528.com)

（2）膜力为主的加载 参考图10-15，如果膜应力相对较高，这时塑性变形只出现在外表面附近，而内表面有σ′_i≤R_eL，通过与上面类似的推导，弹性芯的大小c可以表示为

这时的弯曲曲率是：

这样，在两外表面和内表面的结构应变将具有下列表达式：

于是，伪弹性结构应力是：

式（10-32）与式（10-36）中的伪弹性弯曲应力分量具有相同的表达式，这是因为弯曲应力也只与曲率1/R和杨氏模量相关，如果用一个有效的屈服应力R_e′_L替换上述公式中材料的屈服强度R_eL，那么将很容易地扩展到平面应变问题中。

如果使用冯·米塞斯准则，可用下式的E′替换式（10-32）和式（10-36）中的杨氏模量E，ν是泊松比。

在更近一步考虑带有应变硬化效应的应力-应变曲线的情况下，如果需要求解所产生的结构应变，则要采取数值解析法才能求解。

下面对以弯曲为主的低周疲劳问题的结构应变法求解步骤归纳如下：

1）给定弯曲载荷，给定板厚t，给定材料的屈服强度值R_eL，给定材料的杨氏模量E。

2）先假设是一个弹性问题，根据第5章的公式计算结构应力（其分量是σ_m和σ_b）。

3）由式（10-28）计算弹性芯c，由式（10-27）计算偏移量e。

4）由式（10-30）计算因弹性芯存在而产生的曲率R。

5）由式（10-32）计算考虑塑性的结构应变。

6）由式（10-32）计算考虑塑性的伪结构应力。

7）基于伪结构应力，计算等效伪结构应力。

8）类似于第6章高周疲劳问题的程序，计算给定载荷谱的疲劳寿命。