10.3.1伪弹性应力与LCF数据的处理

首先需要指出：如图10-13所示，ASME标准中的一些低周疲劳的数据明显地落进了与高周疲劳数据具有一致性的窄带里，这些低周疲劳数据大多来自于参考文献[15，16]中所提供的全尺寸的焊管的疲劳测试。

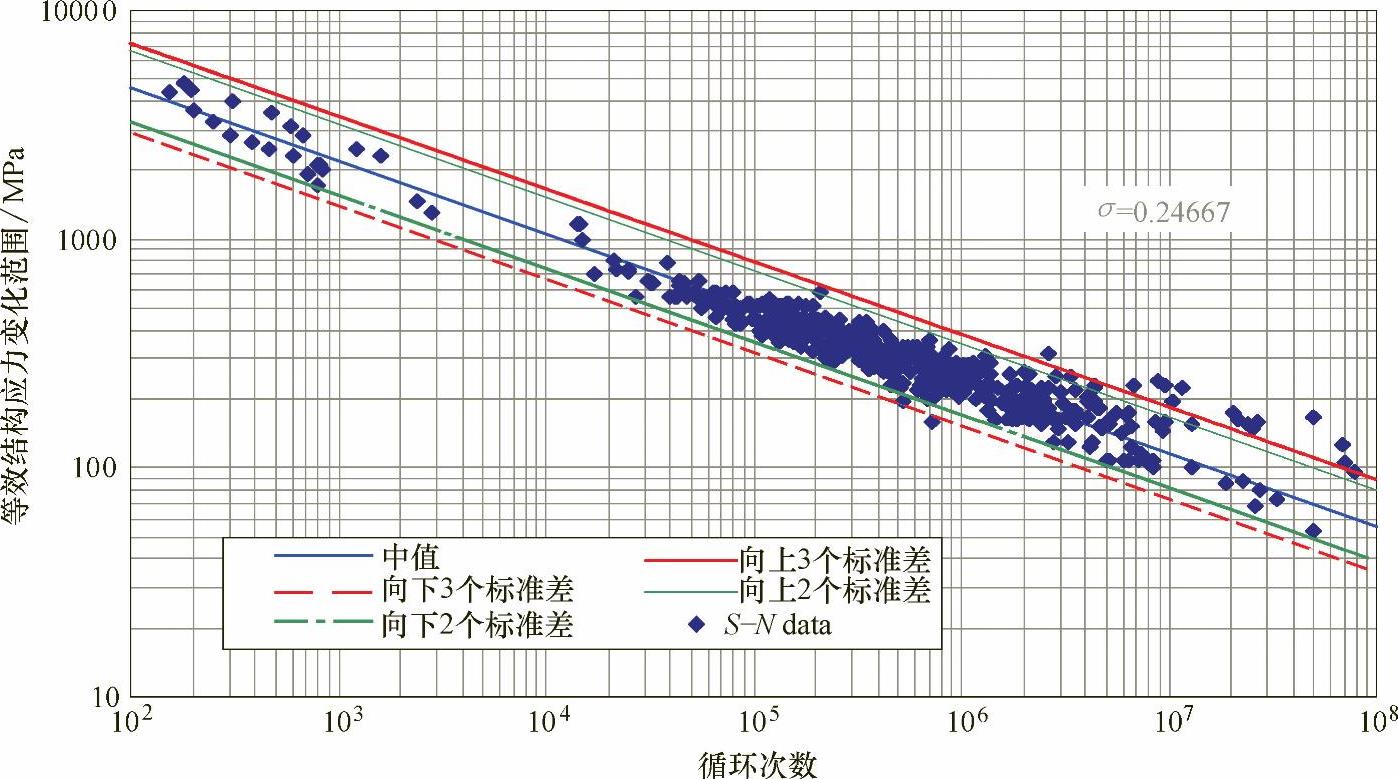
图10-13 低周疲劳数据与高周疲劳数据具有一致性的窄带

利用前面提供的等效结构应力计算方程计算低周疲劳的参数Δσ_s时，直接使用了线弹性策略，不过在那里使用了伪弹性载荷的概念，即将疲劳试验获得的载荷—位移曲线外推插值，获得的是无须进一步处理的伪弹性结构应力。

早在20世纪50年代，Markl就使用了伪弹性应力的概念，图10-14a给出的是位移控制条件下悬臂梁的疲劳试验，图10-14b给出的是位移控制条件下四点弯曲的疲劳试验，图10-14c中给出的δ_a是试验所施加的等幅位移，而F_m则是实际载荷。利用图10-14c所示的外推模式获得了伪弹性载荷F_a，然后利用外推得到的载荷—位移关系曲线，基于弹性梁的应力计算公式就得到了伪弹性载荷对应的伪弹性应力，这个伪应力是伪应变与杨氏模量的乘积：Eε。如果一个构件处于线性弹性范围内，该伪弹性应力实际上就蜕化为该构件中的真实应力。

(www.xing528.com)

图10-14 ASME标准中提供的位移控制的管接头的伪载荷外推插值

对于图10-14给出的管状梁简单弯曲问题，即使塑性变形可能很显著，但是它的载荷—位移曲线依然能够直接被用来说明当应力超出线弹性极限之后的载荷—位移关系。

但是假如塑性变形在某些时候比较突出，那么这时是否还存在有足够尺寸的弹性芯？这就需要根据板壳理论中提供的基本假设给出充分的判断。在关心疲劳问题时，一个测试得到的载荷—位移曲线实际上是可以用来判断以应力为基础的、具有弹性变形的特征对比。此外，低周疲劳时，焊缝上很高的应力集中也将因局部塑性变形而存在。弹性芯的存在确保了这样一个假设的成立，即在应力上升的局部依然由局部应变控制是成立的，而这是由整体变形或者其相对应的伪弹性载荷保证了假设的有效性。

从疲劳评估的角度看，在低周应力区间内，它需要依靠线弹性有限元分析在低周区域的计算。另外，一个低周疲劳评估过程也应该有能力处理载荷控制条件，这是因为与前面提及的受弯曲载荷的简单管接头相比，被评估的部件很可能有一个复杂的几何形状，在这种情况下，疲劳评估时仅有载荷可用，而问题是基于试验的荷载—位移曲线找不到，甚至以计算应力为目的、用来推断伪弹性载荷那样的曲线也找不到。

正是由于上述原因，下面将介绍一种基于解析公式来估计结构应变的方法，即结构应变法，该方法中结构应变的计算是基于应力的，而应力的计算则使用的是来自于线弹性有限元分析得到节点力以后转换得到的结构应力（包括正应力、剪应力）的计算方程。