Sonsino和Kueppers的试验研究及应用分析

在相关多轴疲劳试验数据中，采用MLP法与PDMR法相结合，对试验结果得到了很好的验证，这里仅列举Sonsino和Kueppers报告中管板的角焊缝试验结果进行说明^[8-14]。该实例的焊接接头材料为StE460钢，并作用四种正弦加载条件：纯拉伸、纯扭转、复合成比例的拉伸扭转（同步）、复合相位移90°且不成比例（不同步）的拉伸和扭转，试验设备如图10-9所示，试件如图10-10所示。在名义应力平面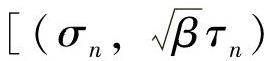平面]上的载荷路径如图10-11a所示，在该图中不同相位的载荷工况是一个圆形载荷路径，且β=3。采用基于网格不敏感的结构应力法计算焊趾处的应力集中系数，拉伸结构应力集中系数为1.7，剪切结构应力集中系数为1.1，这样在图10-11b的结构应力平面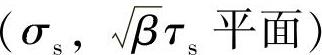上变成了一个椭圆形的载荷路径。

图10-9 试验设备

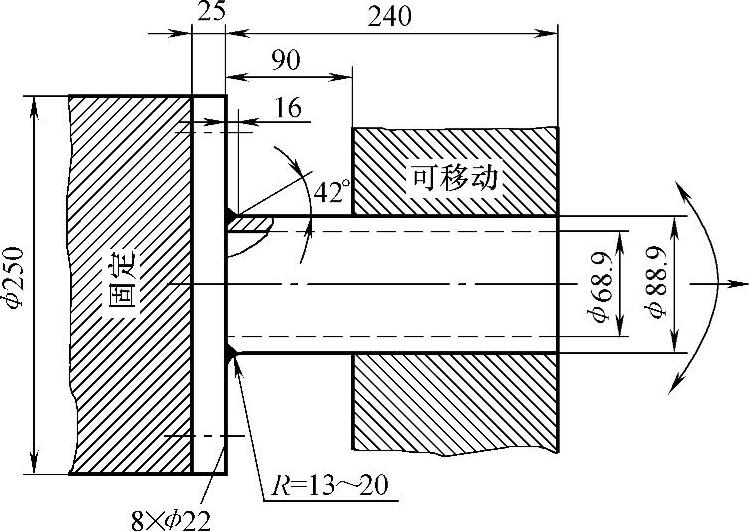
图10-10 试件

根据公式在Sonsion和Kueppers的四种载荷路径中，只有椭圆形载荷路径的非比例系数g_NP是非零的。

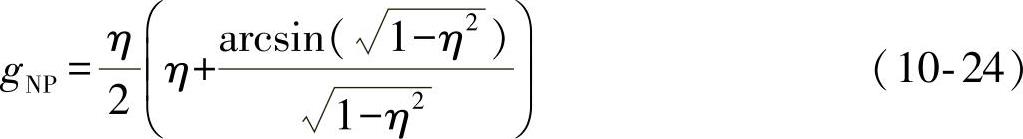
式中，η——椭圆形载荷路径短轴与长轴的比值。

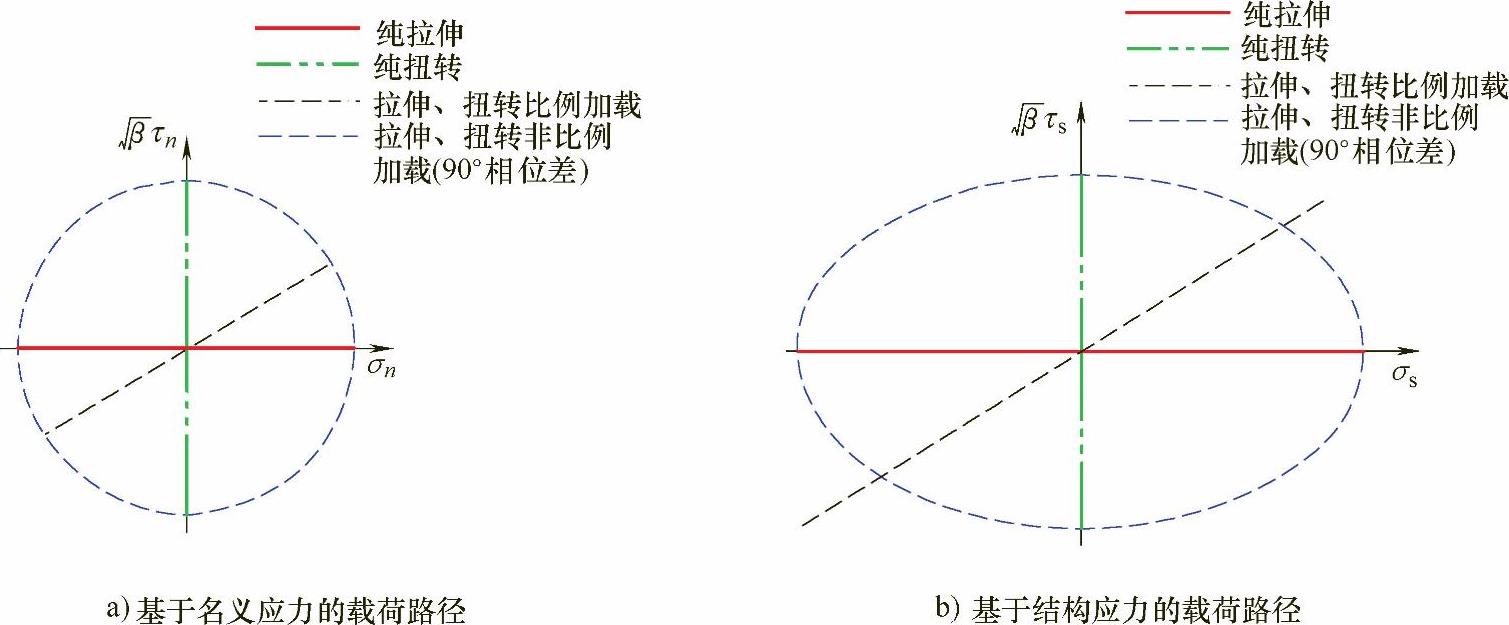
图10-11 Sonsino和Kueppers试验的载荷路径(www.xing528.com)

由于Δσ_e代表平面中最大的直线距离，可以用来计算基于MLP法的等效结构应力范围Δσ_NP，结果如图10-12所示。

如图10-12所示，基于MLP的等效结构应力范围与试验数据有着极好的相关性，S-N曲线数据的标准差仅为0.266，当采用基于PDMR路径长度的等效结构应力参数时，常载荷和变幅载荷的多轴试验数据都落在同一条狭长的窄带内。

综上所述可以得到以下主要结论：

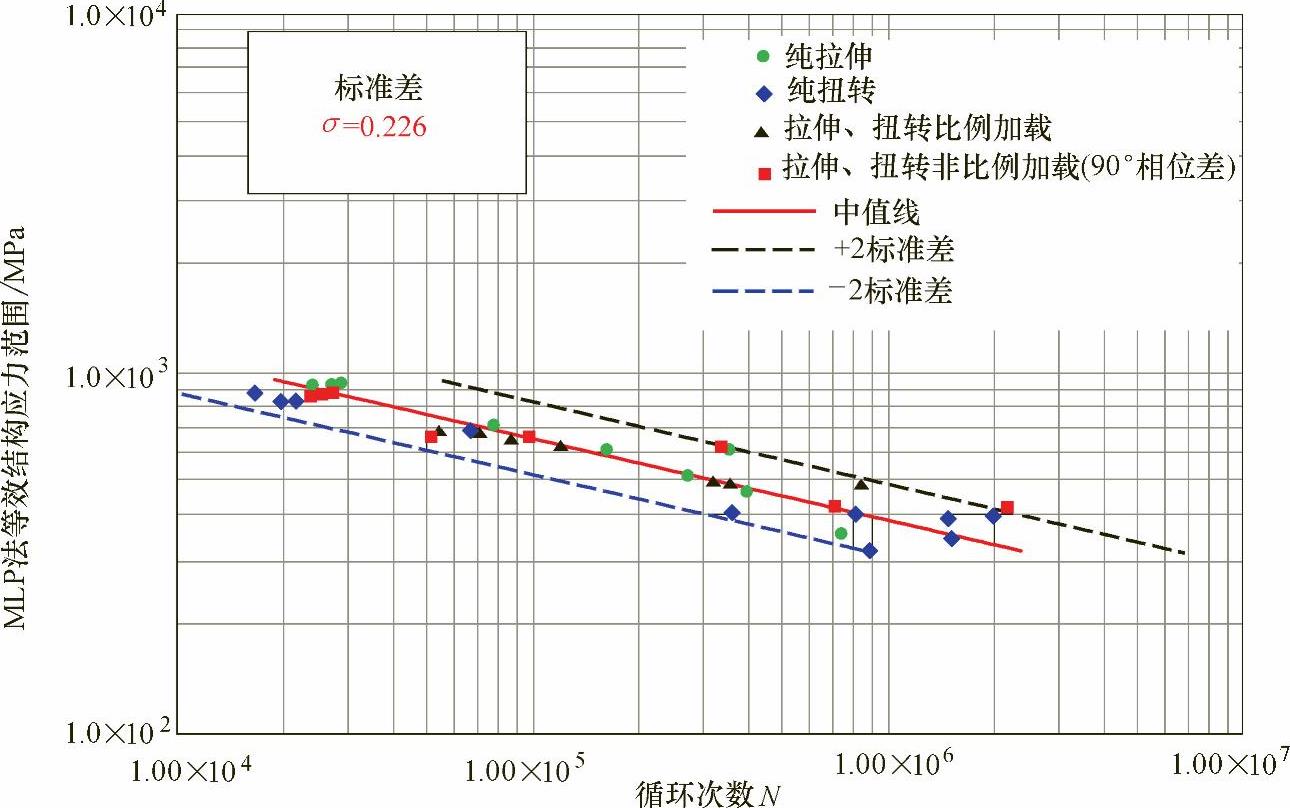
图10-12 基于MLP法的等效结构应力范围与Sonsino和Kueppers试验数据的相关性

1）基于MLP法的疲劳损伤参数，与基于PDMR法的周期计数程序相结合，从相关的不同负载路径模式得到大量的非比例多轴试验数据中证明是有效的。

2）基于MLP法的参数可以被证明是一种积分形式的应变能密度，它是由在给定的非比例加载路径上法向和剪切变形并通过一种路径依赖的函数加权。

3）无量纲的非比例损伤因子g_NP，通过PDMR法循环计数决定的一条路径或者累积路径，相应的每一个半周期的值可以很容易地被计算出来。

4）在变幅多轴疲劳载荷条件下的应力空间或应变空间中，无量纲的非比例损伤因子g_NP，可用于计算基于MLP法的等效应力或者应变参数，并评估多轴状态的疲劳寿命。