剩余寿命评估及等效初始裂纹替代法

如前所述，焊接接头疲劳破坏有两种模式：A模式，从焊趾处开始开裂并穿透板厚；B模式，从焊根处开始开裂并穿透焊缝。从疲劳的角度看，如果焊接接头上有明显的A或B模式的制造缺陷，那么这些缺陷对疲劳寿命究竟有多大的影响，这个问题其实就是工程上所谓的剩余寿命评估问题之一。

理论上焊接结构剩余寿命的评估可以使用断裂力学的知识，但是在结构应力法提出之前的具体操作难度很大，其原因正如前面引用BS7608标准所强调的那样，“如果使用断裂力学定义一个特殊的疲劳寿命，必须格外小心”^[1]。这个担心归根结底是来自于疲劳裂纹的多样性、复杂性，以及分析过程的不确定性而导致的缺口尺寸假设的不唯一性。

现在采用结构应力法可以免除这个担心，因为基于等效结构应力计算疲劳寿命的修正公式中已经考虑了初始裂纹对疲劳寿命的影响，见式（10-1）、式（10-2）。因此如果能将缺陷用初始裂纹定义，那么具有缺陷的结构的剩余寿命就可以被计算出来。

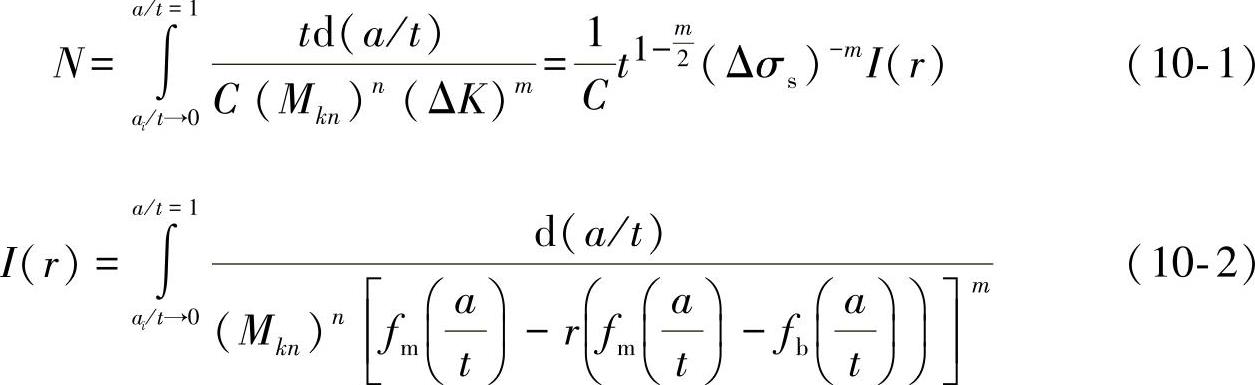
等效结构应力法中关于无量纲积分I（r）^1/m的计算也分两种情况：一是在载荷控制条件下得到，二是在位移控制条件下得到。工程上大量的疲劳测试使用的是载荷控制，并且相应于在载荷控制下得到的积分I（r）^1/m也是谨慎和保守的，因此建议使用载荷控制的式（10-3）。

I（r）^1/m中的被积分项无法直接积分，但是可采用数值方法获得^[2]，拟合以后的非线性方程如下：

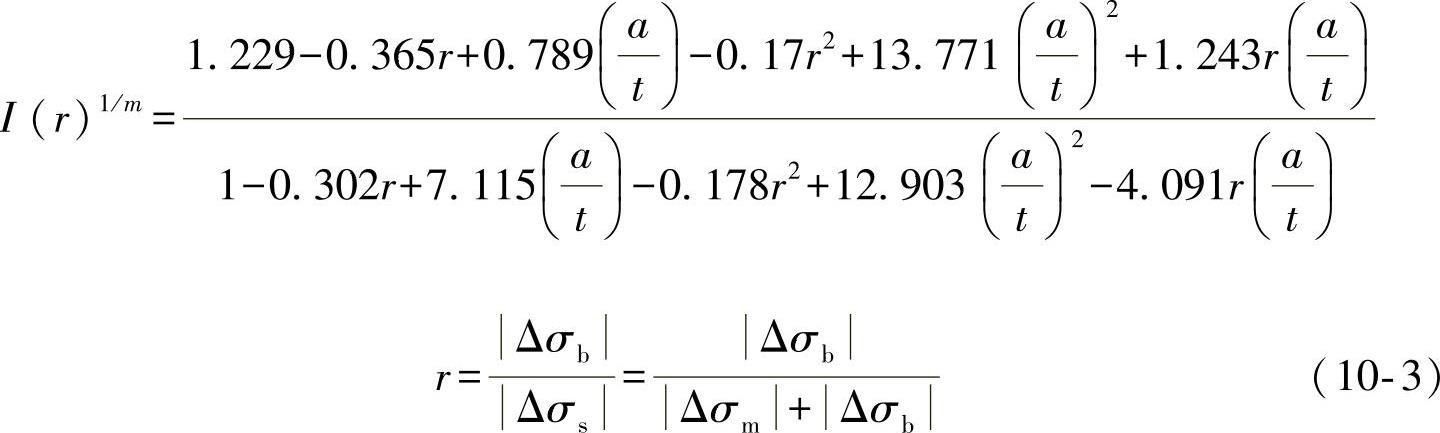
式中 a——初始裂纹深度。

假如没有缺陷或缺陷可以忽略不计，该值默认为接近0，积分区间上限为板厚，即裂纹一直增长到穿透板的厚度。

取不同的a/t值相当于考虑了不同程度的焊接缺陷对疲劳寿命的不同影响，因此可以采用上述方法对含焊接缺陷的构件进行疲劳寿命评估，例如在焊趾的根部存在可以被定性为有削弱作用的缺陷，并且这些缺陷超过了所规定的界限，就要计算缺陷引起的疲劳寿命的缩减。

ASME（2015）标准中规定I（r）公式中适用条件是当a/t≤0.1^[3]，这反映的是正常焊接质量，如果缺陷尺寸超过a/t≤0.1，I（r）公式可作为相对裂纹尺寸用于剩余疲劳寿命评估^[4-6]，注意ASME（2015）标准提供的初始裂纹尺寸最大值是a/t≤0.2，对于更大的裂纹尺寸，式（10-3）的I（r）公式需要重新给定，相关讨论见文献[4-6]。

式（10-3）表明，在计算疲劳寿命时结构应力法具有考虑初始裂纹的能力，并且可以分两种情况研究：

第一种情况，如果焊缝焊趾或焊根的初始裂纹的数值可以用实际测量的方法得到，这样在寿命计算时将实际测量值以积分下限的形式直接代入上述公式即可，因而该种方法被称为“直接初始裂纹法”，焊缝的剩余寿命可以由式（10-1）直接计算。

第二种情况，如果是其他类型的疲劳缺陷，例如未焊透、未熔合、咬边、气孔、夹渣等，它们也是影响疲劳破坏模式的焊接缺陷，但是又不能直接利用式（10-1）计算剩余寿命，这时假如可以用另外的方法将这些缺陷等效为初始裂纹，那么这些缺陷对疲劳寿命的影响及以后的剩余寿命也可以量化计算，这就是“等效初始裂纹替代法”。

对于第一种情况，下面给出一个具体实例。某有咬边缺陷的焊接中梁结构如图10-1所示，图中给出了对接焊缝处咬边缺陷的位置及深度最大值约为3mm。为了评估该初始缺陷对疲劳寿命的影响，基于上述主S-N曲线计算公式得到了剩余疲劳寿命，计算结果见表10-1。

计算结果表明，随着缺陷尺寸a的增加，等效结构应力值随之增大，该处的疲劳寿命随之减少。

(www.xing528.com)

图10-1 有咬边缺陷的焊接中梁结构

为了验证上述剩余寿命结果，利用1500kN多通道电液伺服加载疲劳试验台对含上述缺陷的中梁进行了疲劳试验，如图10-2所示。

表10-1 初始缺陷对应力和寿命的影响

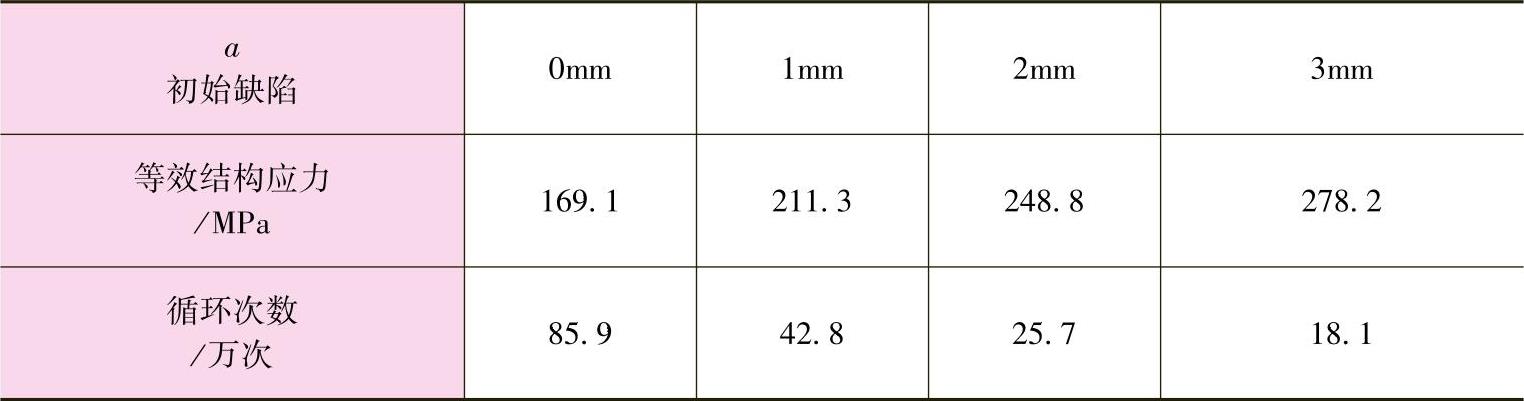
图10-2 中梁在疲劳试验台上的疲劳试验

试验中加载频率为2Hz，施加垂向45t脉动载荷，载荷比为0.1。在加载约17万次时，在含咬边缺陷的对接焊缝处产生了疲劳裂纹，裂纹已穿透板厚，扩展长度约25mm。

可以假定有不同的初始裂纹尺寸，然后计算它们对疲劳寿命的影响。图10-3给出了这些计算结果，其中当初始裂纹为3mm时的疲劳寿命为18.1万次，这一结果与疲劳试验结果很接近，这就证明了“直接初始裂纹法”的有效性。

对于第二种情况，即不能直接获得缺陷具体数值的情况下，推荐使用“等效初始裂纹替代法”。与第一种情况不同的是，该方法需要做一些简单的疲劳寿命测试，下面给出该方法的三个具体执行步骤：

（1）含缺陷样件的制作 制作一定数量的且含有某种质量缺陷的对接接头，缺陷类型可以分别是未焊透、未熔合、咬边、气孔、夹渣等。每一种缺陷对应制作一定数量的对接接头，制作时注意对接板的宽厚比应大于10，以确保焊接残余应力被包括在试验数据里。

（2）疲劳试验 在疲劳试验机上对每个接头进行疲劳加载试验，直到焊缝失效开裂为止，同时记录加载次数，统计得到的平均加载次数，即可定义为有该类型质量缺陷接头的疲劳寿命N。

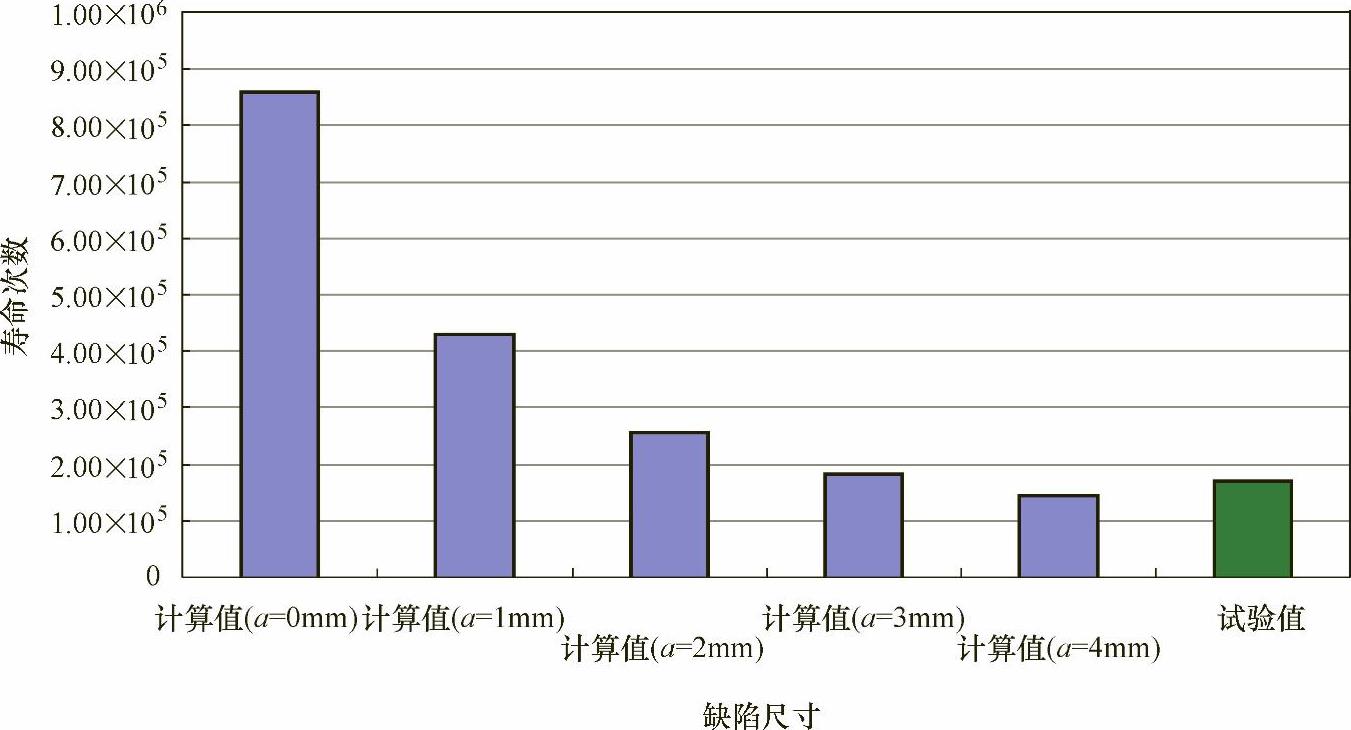
图10-3 疲劳试验寿命与有不同初始裂纹的寿命预测结果的对比

（3）反求初始裂纹尺寸 在式（10-1）中利用已知的疲劳寿命N反求初始裂纹值a。由于N与a之间存在隐式的非线性关系，因此这个过程是反求的试凑过程，一旦试凑结束，与N对应的a值，即可被认为是与该焊接缺陷有对应关系的等效初始裂纹。

“等效初始裂纹替代法”的提出，使得具有焊接缺陷的剩余疲劳寿命预测成为可能，但是在执行这种方法时，疲劳试验样本数量要足够充分，以确保等效结果的鲁棒性。