频域结构应力计算实例详解

仍然取图9-4所示的结构为频域结构应力法考察对象，而疲劳载荷是图9-11所示的随机载荷时间历程。通过傅里叶变换可获得载荷功率谱。根据图9-12可以看出A点的等效结构应力功率谱响应在7.4Hz处出现峰值，这说明随机载荷激起了结构的一阶模态振动。

从图9-13可以看出A和B两点疲劳寿命最短，这表明频域结构应力法能够直接考虑随机载荷对疲劳寿命的影响。

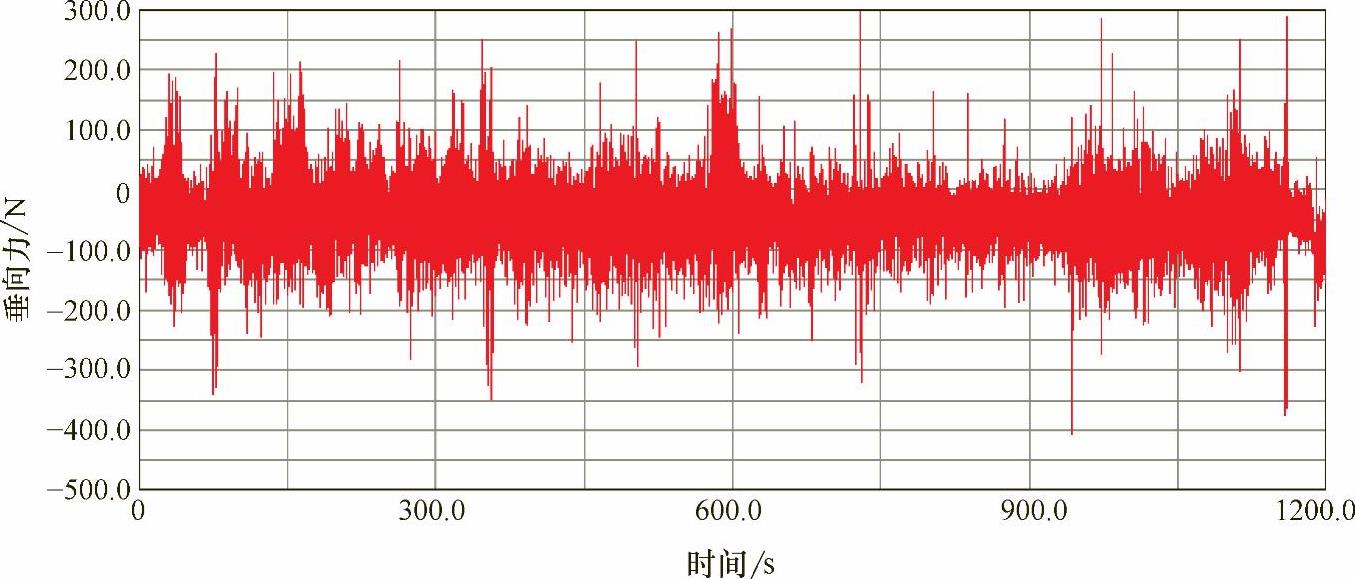
图9-11 随机载荷时间历程

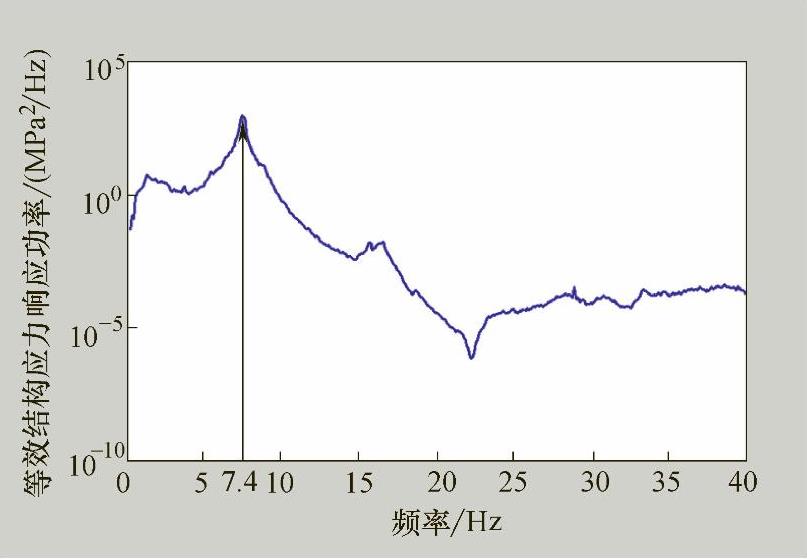
图9-12 A点的等效结构应力响应功率谱

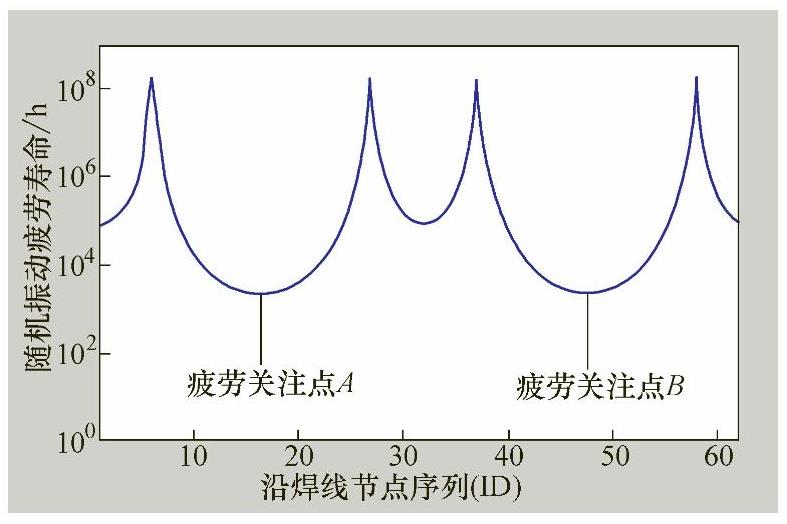
图9-13 随机载荷作用下环形角焊缝疲劳寿命预测

下面给出频域结构应力法的实际工程应用案例。在恶劣线路上服役不久的某铁路集装箱平车的焊接结构上，一个并没有载荷直接作用的辅助梁焊缝发生了疲劳开裂，如图9-14所示。在实际运营的线路上对该车进行振动加速度实测，测试数据表明该车车体结构振动现象严重。

首先，创建含焊缝结构的有限元模型，图9-15是疲劳开裂处的局部模型。加速度谱中最重要的是车体前后心盘处的横向与垂向加速度谱，因为它们是随机振动计算的输入条件。图9-16和图9-17给出的是实测的垂向加速度谱。利用傅里叶变换将这些数据转换到频域，图9-18和图9-19给出的是垂向功率谱，通过前后心盘处加速度频域分析，可得出车体所受载荷的频域能量分布。为了考虑车体前后心盘横向和垂向加速度载荷之间的耦合作用，需要得到对应的互功率谱。图9-20所示的实测得到的互功率谱包含载荷间的相位信息。图9-21、图9-22分别给出了计算结果与实测结果的对比，图9-23给出了疲劳失效位置等效结构应力响应的功率谱。

图9-14 辅助梁焊缝疲劳开裂照片

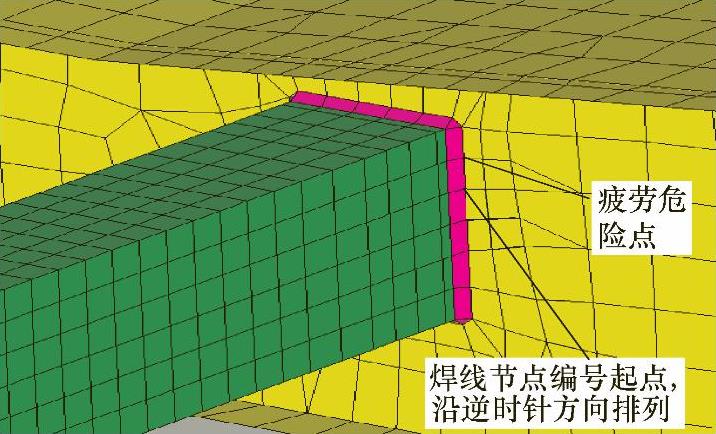
图9-15 焊缝细节模型及焊线定义

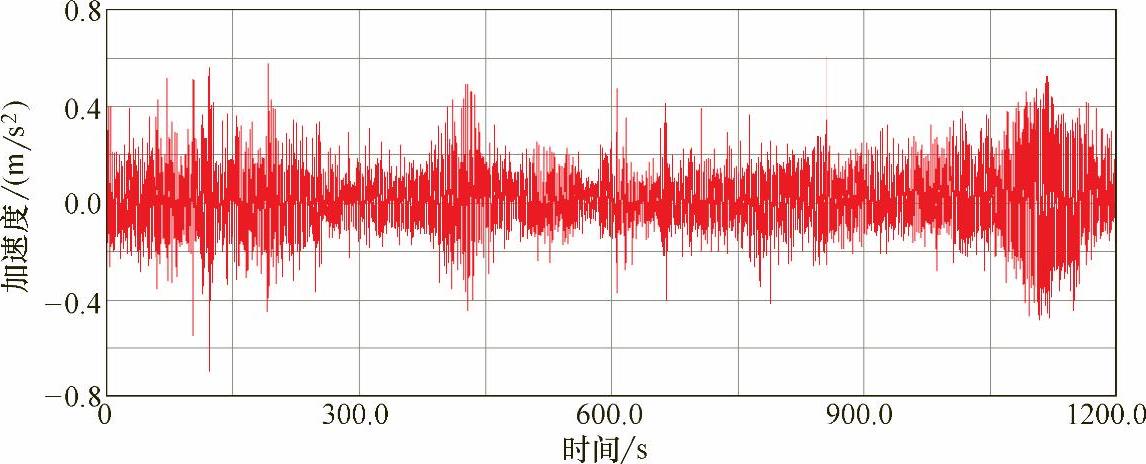
图9-16 前心盘处垂向加速度时间历程(www.xing528.com)

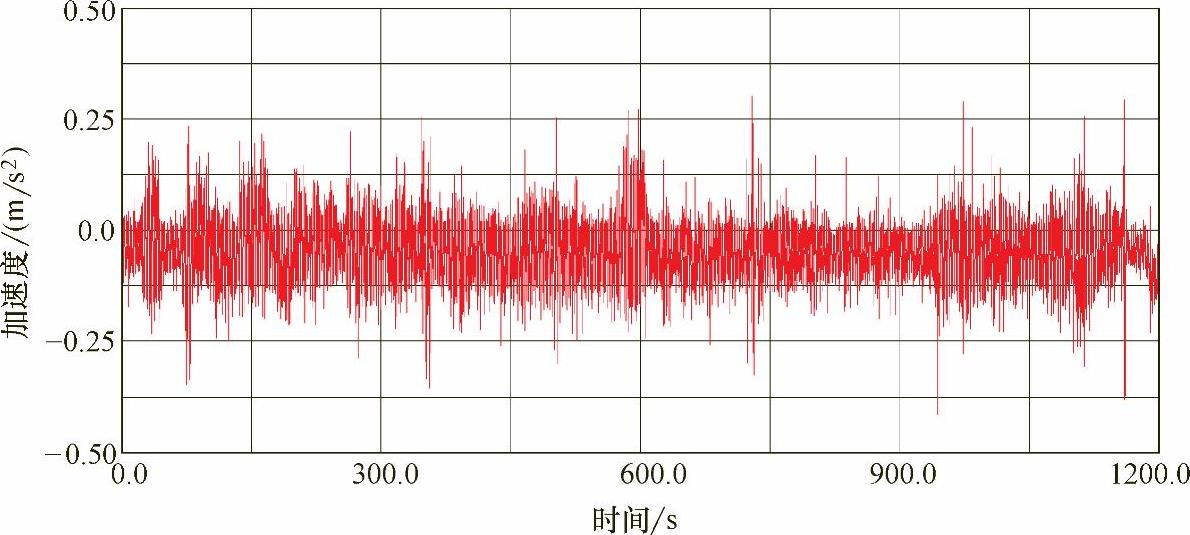
图9-17 后心盘处垂向加速度时间历程

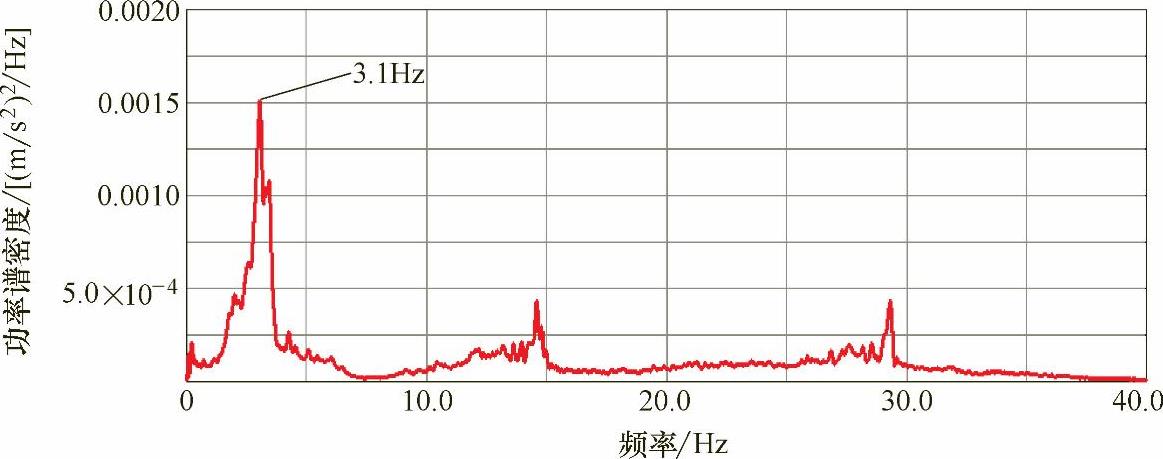
图9-18 前心盘处垂向加速度功率谱密度

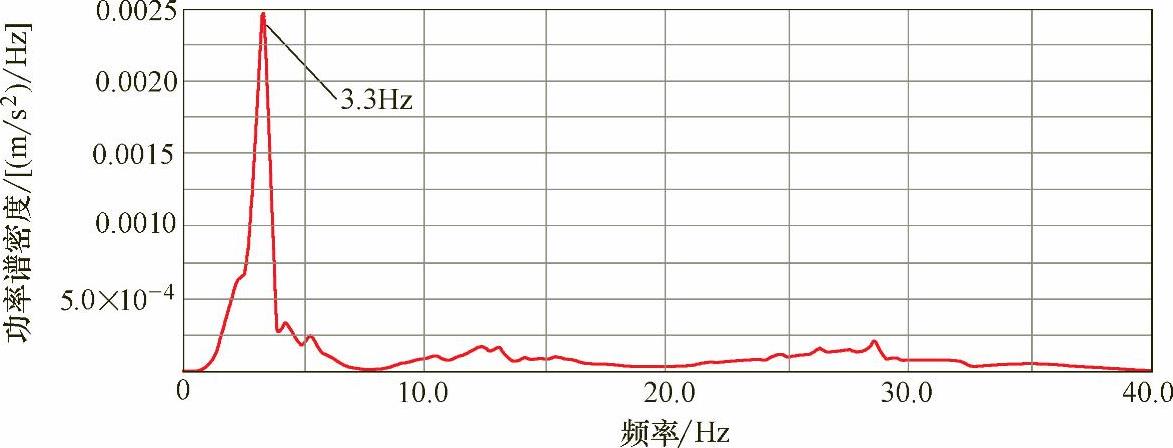
图9-19 后心盘处垂向加速度功率谱密度

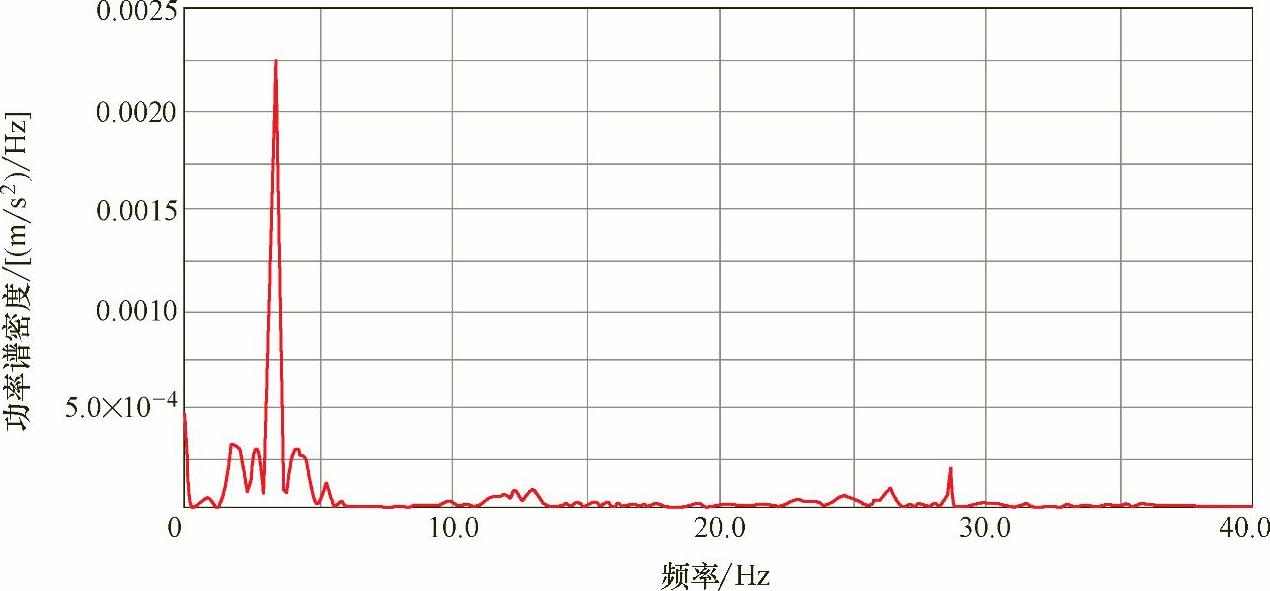
图9-20 前后心盘加速度互功率谱密度

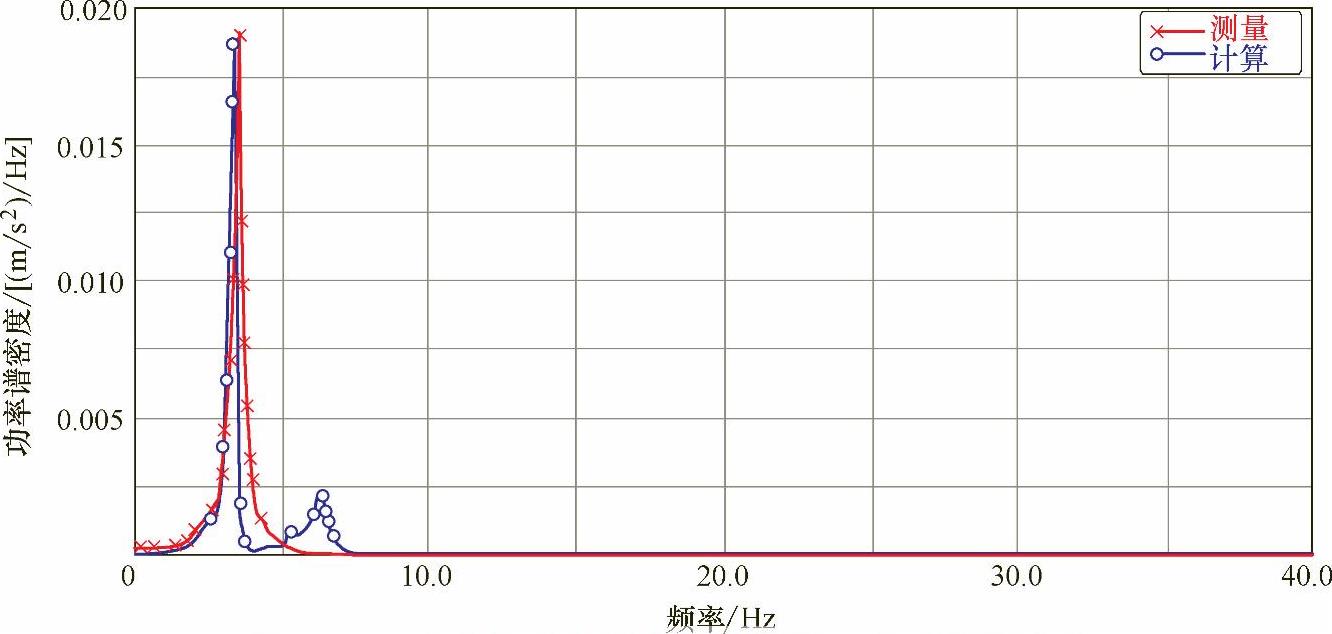
图9-21 垂向加速度响应计算结果与实测结果对比

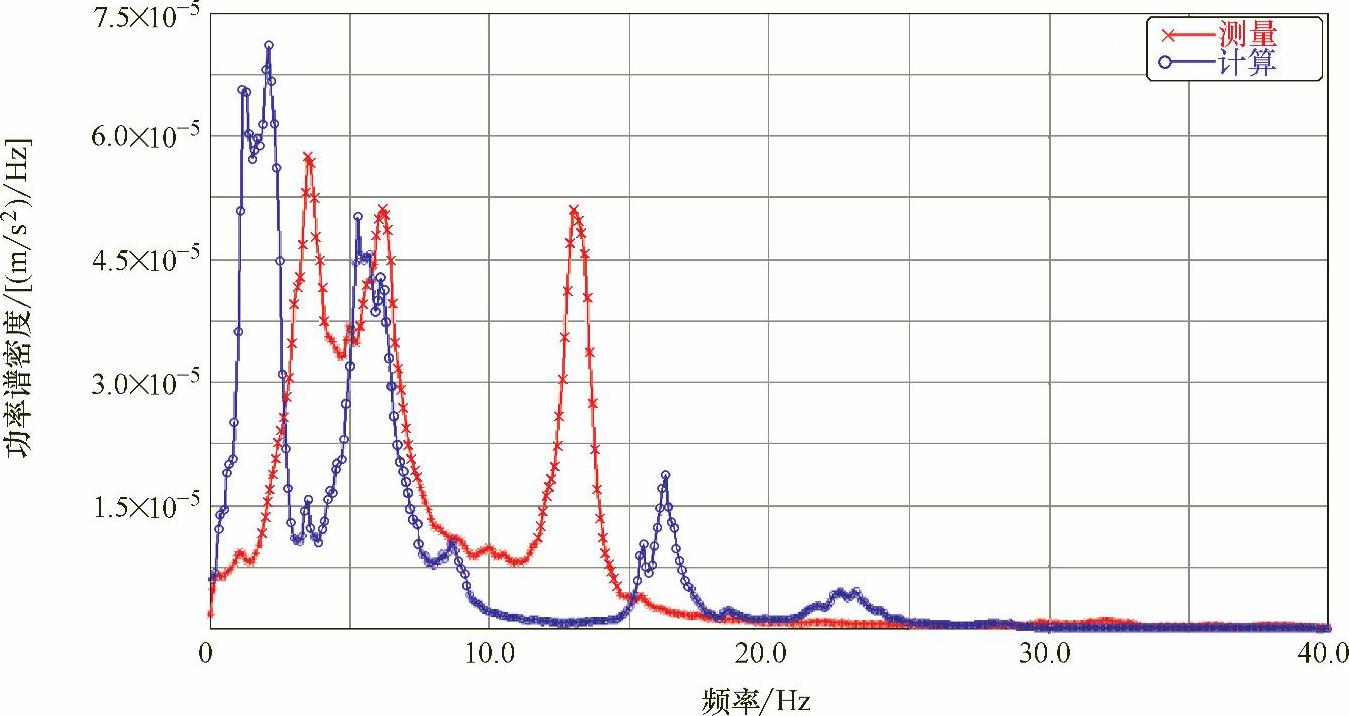
图9-22 横向加速度响应计算结果与实测结果对比

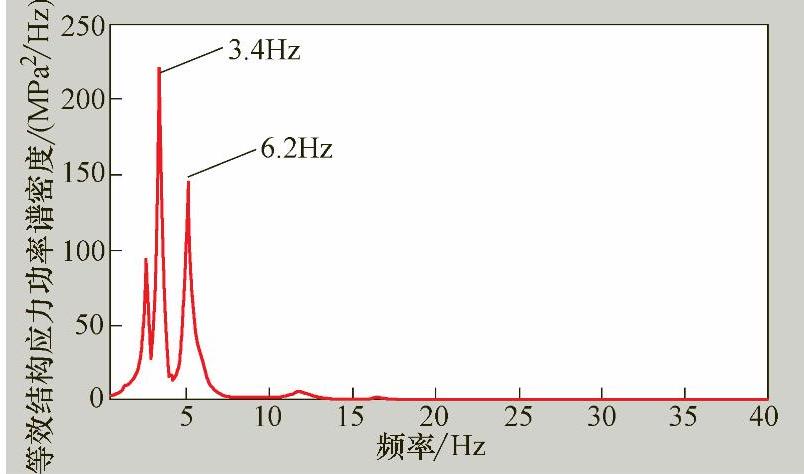
图9-23 疲劳危险点的等效结构应力响应功率谱

预测结果显示疲劳寿命最低位置发生在边梁的上表面焊接处，且该边梁的下表面也是疲劳薄弱部位，这与实际发生开裂位置一致，焊缝疲劳寿命也基本吻合，根据计算结果进行了结构局部改进，这个问题因而得到了解决。