频域结构应力的推导及疲劳评估

1.计算频域节点力

首先，位移频率响应函数H（ω）取决于结构的固定参数如质量、刚度、阻尼等，而与外载荷无关，是结构系统的固有特性。求解有限元模型之后得到的是一系列的随频率变化的节点位移向量组。但是频域与时域计算不同，因为频域位移频率响应函数是复数形式，因此频域结构应力需要将实部与虚部分开讨论。

以下推导的关于频域结构应力是关于实部的，由于虚部的推导方式与实部类似，不再重复介绍。

类似时域的方法，先通过坐标变换获得全局坐标下的单元刚度矩阵。

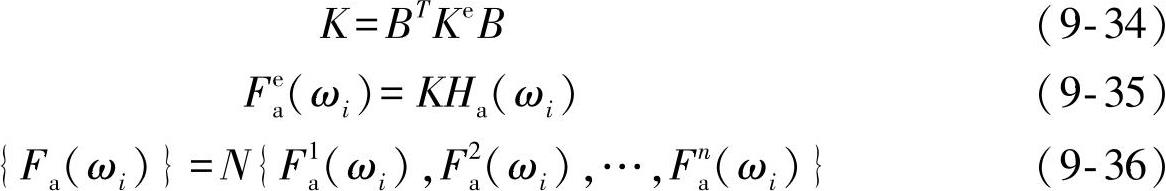
式中 ω——频率；

H_a（ω_i）——复频响应H（ω_i）中与单元e对应的位移向量的实部；

{F_a（ω_i）}——节点力向量的复频响应实部；

其余符号同前。

2.节点力坐标变换

类似时域的做法，系统坐标系下的焊线节点力、力矩矩阵也需要通过坐标变换将它们变换到基于焊线的坐标系中。

{f_a′（ω_i），m_a′（ω_i）}=T{F_a（ω_i）} （9-37）

3.计算等效线力和线力矩

还是按照时域的做法计算等效线力和线力矩：

{f_a（ω_i）}^T={f_a′（ω_i）}^TL^-1 {m_a（ω）}^T={m_a′（ω_i）}^TL^-1 （9-38）

4.计算结构应力频率响应函数

因为已经获得了焊线各节点线载荷及线力矩，使用结构应力计算公式可以获得焊线各节点结构应力的频率响应函数的实部。

式中 t——板厚。

将前面获得的等效线力和线力矩代入式（9-39），从而可获得结构应力的频率响应函数的实部。

H^a_σ（ω_i）={TNB^TK^eBL^-1A}H_a（ω_i） （9-40）

同理，可以获得结构应力的频率响应函数的虚部。(www.xing528.com)

H^b_σ（ω_i）={TNB^TK^eBL^-1A}H_b（ω_i） （9-41）

最后可以获得离散的频域结构应力的复频响应函数。

H_σ（ω_i）=H^a_σ（ω_i）+H^b_σ（ω_i）j （9-42）

频域下的结构应力与特定频率下的载荷之间存在线性传递关系，可以利用随机振动相关的理论计算随机载荷作用下焊缝处的结构应力响应。由于最终利用主S-N曲线进行焊缝寿命预测的是等效结构应力参数，因此需要获得等效结构应力的频率响应函数及其在随机载荷作用下的振动响应才能用于疲劳寿命预测。

5.等效结构应力频率响应函数

根据ASME标准中提供的等效结构应力计算公式，可获得频域下的焊线上各节点等效结构应力的频率响应函数。

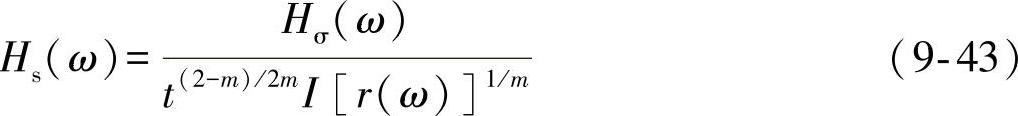
式中 I[r（ω）]——频域下的弯曲比。

前面已经证明了频域下结构应力与频域载荷之间存在线性传递关系，因此频域下弯曲比与频域载荷之间也存在线性传递关系。在频率为某一确定值时，频域弯曲比等都是常数，所以在给定的频率下弯曲比不变，这样一来，频域等效结构应力与结构应力的力学机制一样，与频域载荷之间也存在线性传递关系，而H_s（ω）则定义为等效结构应力的频率响应函数。

6.等效结构应力频率响应功率谱

根据随机振动理论，线性振动系统的响应可以利用单位载荷的频率响应函数与实际作用在结构上的载荷功率谱的乘积来获得，在多通道载荷的情况下，由于相位差的存在，需要考虑载荷之间的互功率谱。

基于载荷的自功率谱S_ii（ω）、载荷之间的互功率谱S_ij（ω），以及前面已经获得的等效结构应力频率响应函数，这样就可以获得焊线上每个节点的等效结构应力响应功率谱。

式中 Hⁱ_s（ω）——第i个载荷通道对应的等效结构应力频率响应函数。

7.疲劳损伤统计

等效结构应力变化范围是主S—N曲线公式中的一个参量，而Dirlik法可以对某个随机物理量的功率谱进行统计而获得该物理量的概率密度函数^[3，4]，因此基于Dirlik法对等效结构应力功率谱进行统计，就可以获得以单位时间度量的不同等级的应力变化范围的发生次数。

根据Miner疲劳损伤累积原理可以计算出单位时间内焊线上某一点的疲劳损伤值。

因为式（9-45）计算得到的是单位时间的疲劳损伤累积值，那么在给定的服役时间内，就可以推算出焊线上该点的总损伤值。假如一年的损伤值是0.04，如果规定的总损伤值为1，那么寿命就是25年。如果需要，该值还可以很容易地换算为服役里程数，按照这个流程，就可以统计出某条焊线（实际焊缝的焊趾）上所有点的疲劳损伤或寿命分布。以轨道车辆的随机振动为例，上述步骤归纳之后可以用框图的形式给出每个步骤的入口与出口。图9-10为基于频域结构应力的疲劳寿命预测流程。

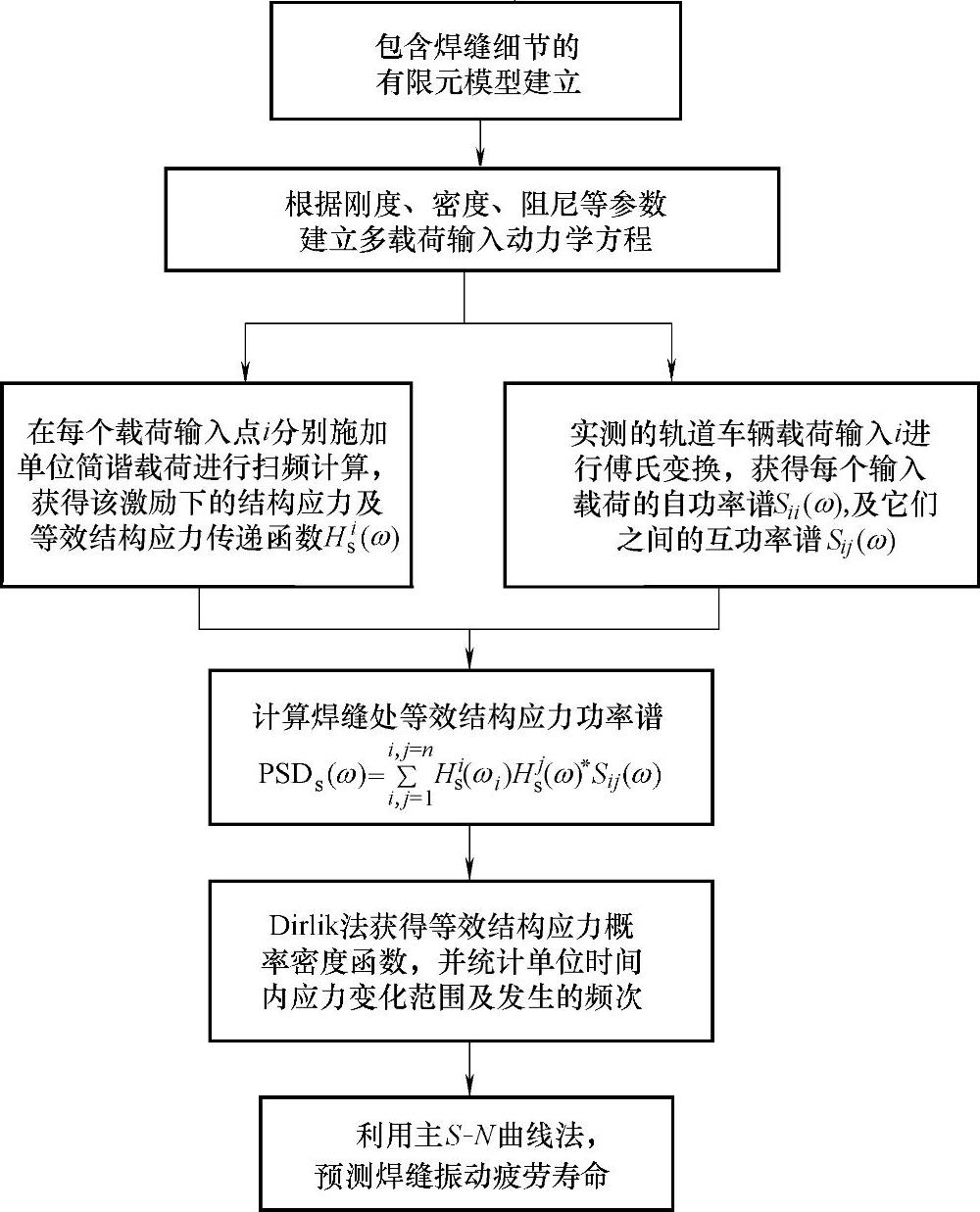
图9-10 基于频域结构应力的疲劳寿命预测流程