获取焊接接头上疲劳载荷的子结构技术优化方案

上一节讨论的是焊接结构全局性疲劳载荷的获取，然而这一载荷并不等价于每个焊接接头的疲劳载荷，那么每个焊接接头上局部性的疲劳载荷该从哪里来呢？为了解决这个问题，可以考虑使用有限元方法中的子结构技术。

子结构技术实质是将计算规模很大的结构中切割出一个或多个子结构，然后将每个子结构内部的自由度凝聚到切割以后形成的边界上，自由度凝聚以后，原问题的求解规模将明显减小从而提高计算效率。许多有限元法的专著中都有关于子结构技术的细节介绍，这里不再赘述，下面仅简要介绍其自由度凝聚过程^[4]。

假设一个子结构上的所有节点位移因切割可被分成两部分：U₁是切割边界上的位移，U₂是其内部位移，于是这个子结构的求解方程就对应成以下形式：

式中 K_ij——与位移对应的刚度矩阵；

F_i——对应的载荷向量。

将式（7-1）展开，可以得到：

K₁₁U₁+K₁₂U₂=F₁

K₂₁U₁+K₂₂U₂=F₂ （7-2）

由式（7-2）得：

U₂=K₂₂^-1（F₂-K₂₁U₁） （7-3）

将式（7-3）代入式（7-2），整理后有：

式（7-4）即为凝聚以后的求解方程，其中：

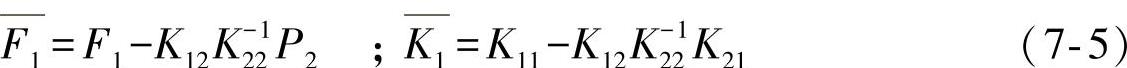
事实上，在这里提及子结构技术的原因是：每个子结构求解以后，被切割面上所有节点的力也被同时求出来了，这些切割面上的信息被整理后即可转化为被切割面上的合力。如果子结构是依据焊接接头的几何而定义的，那么这个切割面上的合力即为系统载荷传递到该焊接接头上的载荷，这一点对非标准焊接接头尤其重要。

在运用子结构技术之前，首先进行结构静强度校核，一旦静强度设计要求得到满足，再进入疲劳强度校核阶段提取所需要的节点力，具体执行步骤如下。

第一步：按照事先约定的焊接接头的三维几何，在有限元模型中定义子结构。

第二步：从每一疲劳载荷工况中确认载荷最大值。

第三步：对每一载荷最大值的整体结构求解。

第四步：利用子结构技术，分别提取与每一最大载荷值对应的子结构切面上的每一个节点的节点力分布。

第五步：对切割面上节点力进行合成，获得每一个切割面上的合力分布。

第六步：利用线性换算关系，获得与每一疲劳载荷波形对应的切割面上的节点力波形以及合力波形。(www.xing528.com)

第七步：将这些波形作为每一个焊接接头上的疲劳载荷谱存储。

下面以某转向架焊接构架为例，如图7-1所示，按照上述步骤给出用子结构技术计算非标准焊接接头的疲劳载荷的具体方法。

图7-1 基于子结构技术定义的焊接接头示意

1）假设需要研究的对象是横梁与侧梁的连接部位，接着以CAD软件为工具切割出如图7-2所示的三维几何，该三维几何既可视为一个非标准焊接接头，也可以视为有限元的一个子结构。

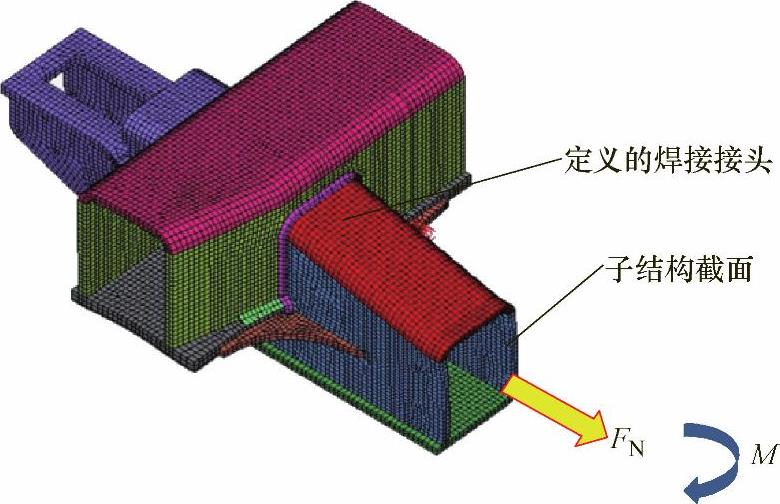
图7-2 子结构及焊接接头载荷

2）根据该结构的几何，应用工具软件（例如Hypermesh）创建其有限元模型，其中含焊缝单元。

3）根据UIC 515-4标准对整体结构施加载荷，然后基于子结构技术求解以获得子结构切割面上的节点力。

4）设计计算程序，将切割面上的节点力转化为如图7-2所示的截面合力。

下面通过一个案例给出基于子结构技术获得某焊接构架上非标准焊接接头截面内力的过程。

首先根据对称性取一半结构计算，对称面上施加对称约束。根据UIC515-4标准对结构施加疲劳载荷，有限元网格及载荷如图7-3所示。

图7-3 有限元网格及载荷

然后，在有限元模型中定义一个非标准的焊接接头，该接头有三个截面，如图7-4所示。

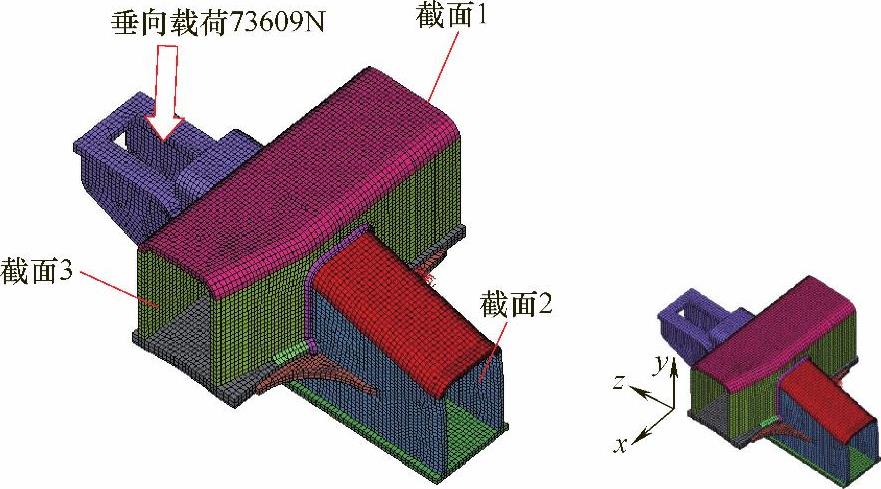
图7-4 有限元模型中定义焊接接头的三个截面

接着，将有限元模型导入ANSYS软件进行静力计算，然后在ANSYS软件后处理模块提取接头各截面上节点的节点力，并将节点力转化为截面上的合力。每个截面上得到6个内力，包括截面轴力、两个方向的剪力、截面扭矩和两个方向弯矩。

在图7-4所示坐标系下，表7-3列出了该非标准接头截面内力计算结果。

表7-3 非标准接头截面上力及力矩的计算结果

因为结构具有线弹性，因此按照整体结构疲劳载荷的波形很容易获得接头上的疲劳载荷波形。