计算等效结构应力和主S-N曲线公式

由于将裂纹扩展过程划分为短裂纹和长裂纹两个阶段，下面可以采用统一的Paris公式将短裂纹增长与长裂纹的增长统一起来。

da/dN=C（M_kn）ⁿ（ΔK_n）^m （6-14）

对式（6-14）进行积分，可以得到从小裂纹到穿透厚度t的疲劳寿命预测表达式：

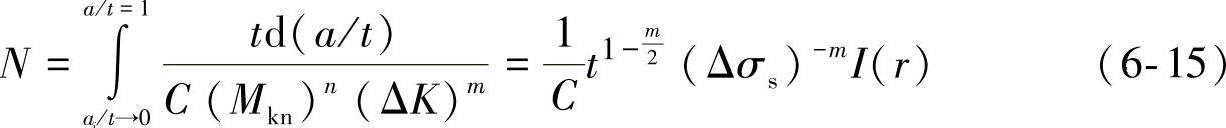
式（6-15）中ΔK为应力强度因子变化范围，其表达式为

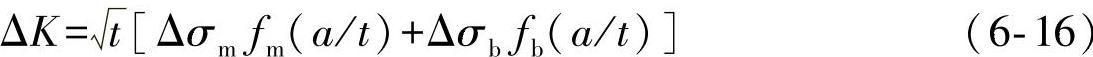
f_m（a/t）和f_b（a/t）与式（6-1）中的形状参数f_m及f_b相同，分别为膜应力和弯曲应力单独作用时确定应力强度因子范围的无量纲函数。

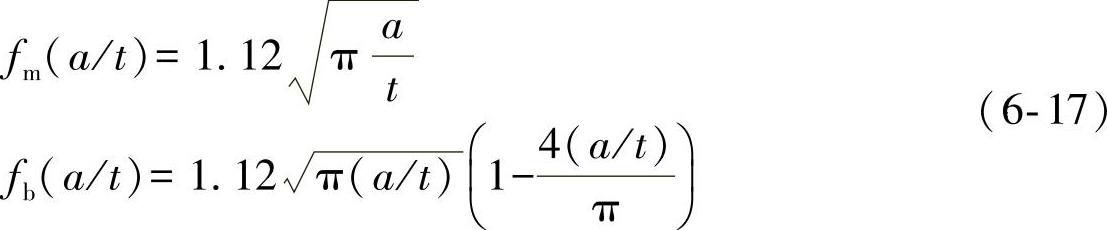
I（r）为载荷弯曲比r的无量纲函数。

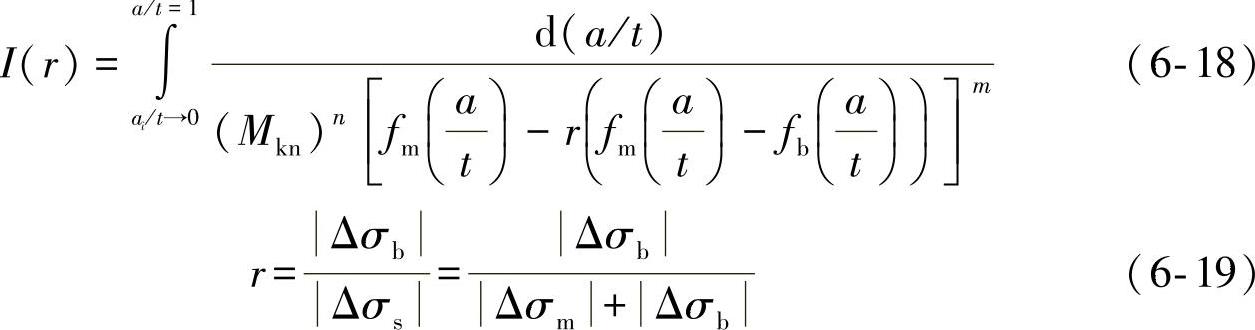
式中 Δσ_m——膜应力变化范围；

Δσ_b——弯曲应力变化范围。

令：

理论上，由式（6-15）可以计算出寿命，但是从工程应用的角度出发，式（6-15）中的两个常数需要用大量的疲劳试验数据修正，数据拟合修正以后的计算公式为式（6-21）。

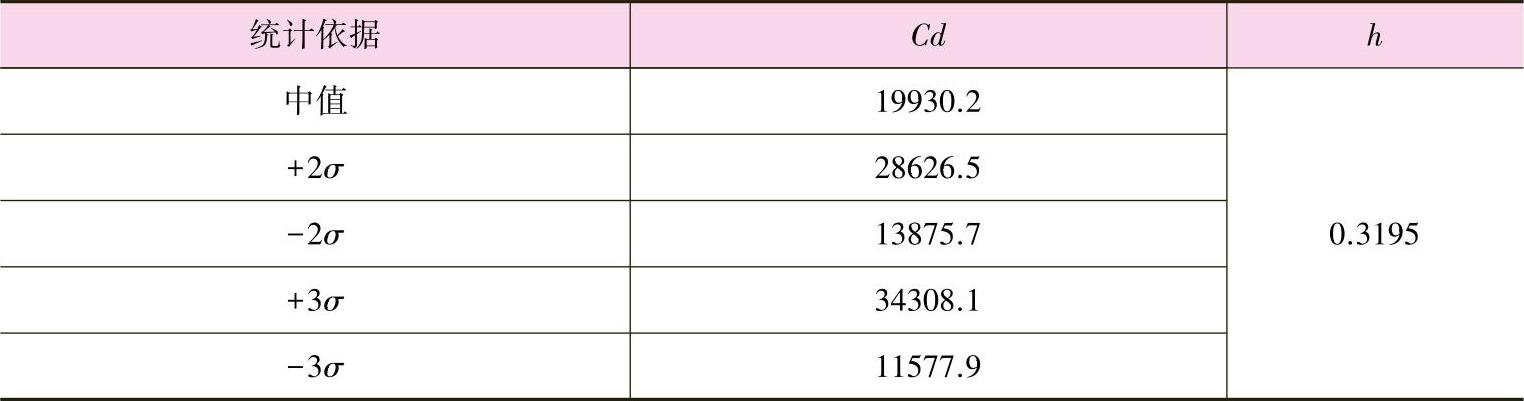
N=（ΔS_s/C_d）^-1/h （6-21）

式中 C_d，h——表6-1中的试验常数。

式（6-20）中的I（r），因采用解析法求解困难，所以一般通过数值拟合的方法获得。

这里需要强调指出，I（r）中含初始裂纹参数，而初始裂纹尺寸能够对最终寿命预测结果产生重大的影响，关于这一点将在第10章中进行讨论。

还应当指出，迄今为止所讨论的应力强度因子的解决方案都是基于载荷控制条件的，即：在疲劳裂纹的整个生命周期中，都是用结构应力来表现的，但是使用结构应力的位移控制K解的简单估计来考虑焊接残余应力对疲劳寿命的影响时，其精度已被证明是足够好的。

在某些试验条件下，是应该考虑位移控制条件的。然而，到目前为止所发表的大多数的文献数据都是基于载荷控制条件的。正如董平沙教授所讨论的那样，结构应力的位移控制解决方案是充分考虑焊缝残余应力的正确方法。图6-5给出了这样的一个证明。

在位移控制条件下的K值的求解已被三维有限元方法（FEM）证明是可行的^[2]，它不考虑弯曲分量σ_b的载荷控制条件下半无限体的典型的边缘裂纹解决方案。图6-5说明了在纯弯曲工况下，K在载荷控制条件下与位移控制条件下性能的不同，当裂纹尺寸a/t非常小时，两种解决方法在本质上是相同的。当裂纹尺寸a/t增长到大于0.1（临界深度）时两种方案开始相互偏离，与载荷控制条件相对应的K作为裂纹尺寸的函数单调递增，而与位移控制条件相对应的K迅速下降，并在a/t=0᤼8时降到0。

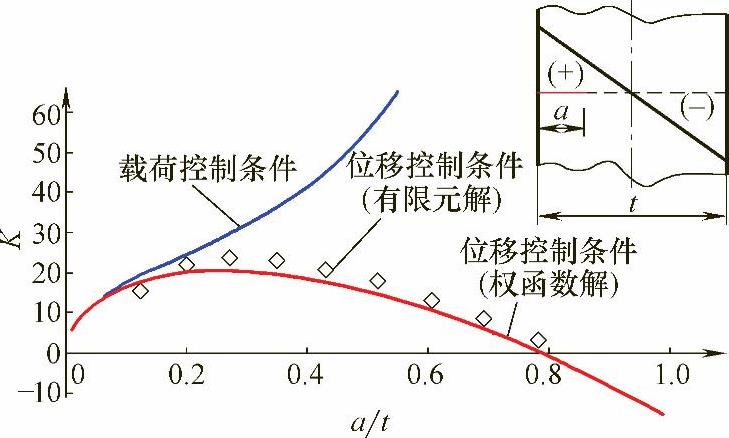
图6-5 在载荷控制条件下与位移控制条件下的K解

图6-6给出了数值求解I（r）得到的拟合曲线。试验数据表明，在位移控制条件下的焊接接头疲劳寿命要高于载荷控制条件下的寿命，在载荷控制条件下，a=0时I（r）可拟合为式（6-22），在位移控制条件下，I（r）可拟合为式（6-23）。

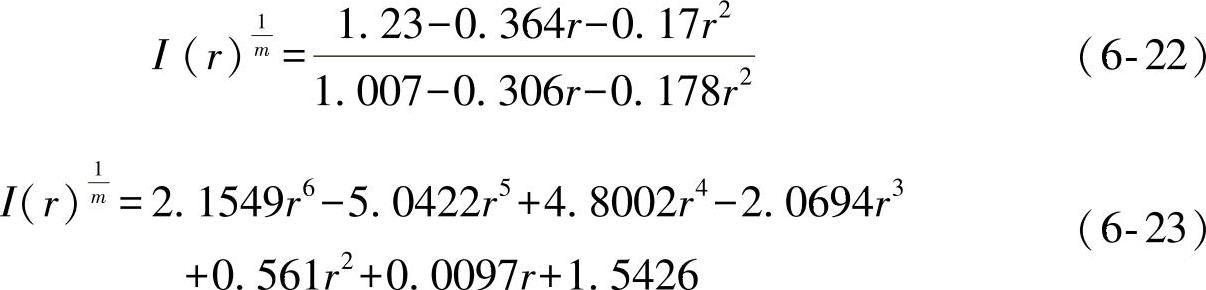(www.xing528.com)

式（6-21）非常重要，由于它是基于结构应力推导而得到的，因此可以将其命名为基于结构应力的疲劳寿命计算公式，式中ΔS_s是等效结构应力变化范围的数学表达式。从式（6-20）中可以看出，等效结构应力变化范围是三个参数的综合：结构应力变化范围Δσ_s、板厚t、描写膜应力与弯曲应力状态的I（r）。

至此，如果将式（6-21）改写为：N=C₀/（ΔS_s）^1/h，然后将它与基于名义应力的疲劳寿命计算公式N=C/（Δσ）^m放在一起，会发现这两个计算疲劳寿命的公式形式上非常相似，分子均是由试验确定的常数项，分母均是由外载荷确定的应力项，只不过是名义应力法中以名义应力变化范围为参数，结构应力法中以等效结构应力变化范围为参数。考虑到两个S-N公式的相似性，因此式（6-21）也被命名为主S-N曲线方程。

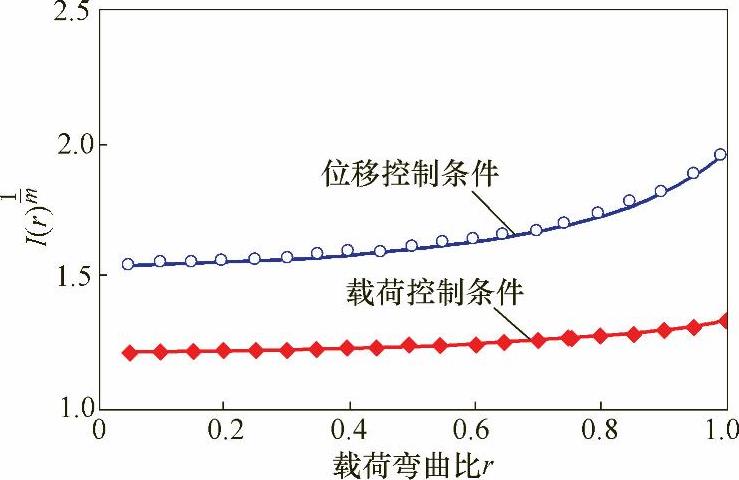
图6-6I（r）的拟合曲线

等效结构应力ΔS_s可以用来把不同的接头形式、厚度、加载模式的疲劳S-N数据有效地统一起来。图6-7给出了用等效结构应力将不同类型的S-N数据的有效统一。

同时从图6-7的统计中也证明了断裂力学中用把疲劳损伤过程当作裂纹扩展过程的方法来解释大量不同接头类型的S-N数据时的优势，更重要的是，就ΔS_s-N而言，从各种不同类型的接头形式、加载方式已经证明了主S-N曲线的存在。

为了验证主S-N曲线方程的有效性，美国Battelle试验中心对比分析了自1947年以来的近1200个焊接疲劳试验的数据。在图6-8所示的数据中，包括了下列重要信息：

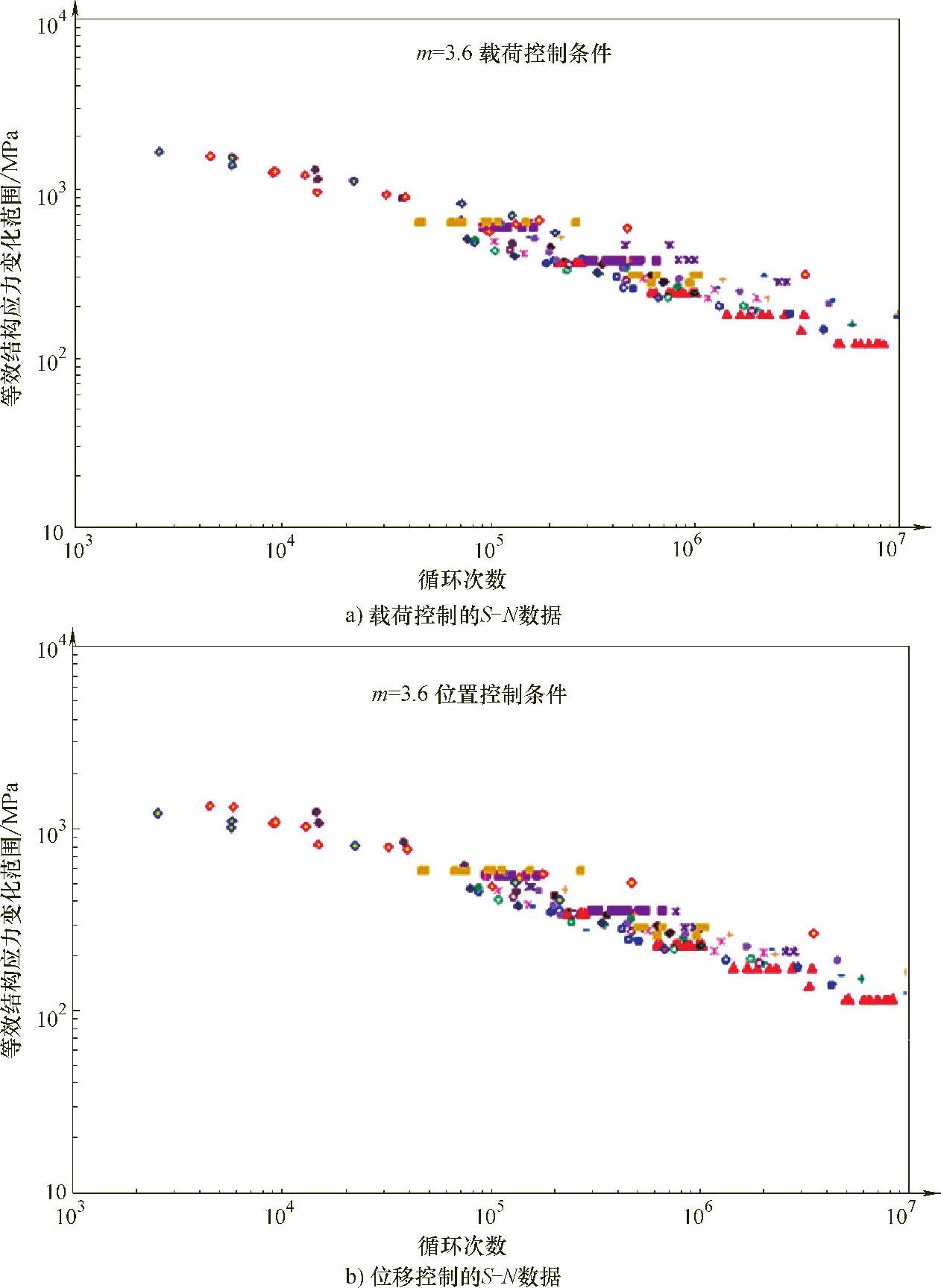
图6-7 不同类型的S-N数据的统一

注：图中符号代表不同样件的实验数据。

1）材料：钢的屈服强度的范围为180～1200MPa；

2）板厚的变化范围为1.5～104mm；

3）接头类型有T形接头、搭接接头、十字接头、纵向加强肋焊缝、电阻点焊等；

4）载荷条件：纯远端拉伸、纯远端弯曲以及二者之间的不同组合。

如图6-8所示，以等效结构应力变化范围ΔS_s表达的S-N曲线数据分布范围狭小，这就意味着基于名义应力的试验数据在考虑了三个因素之后都被压缩到一条窄带中，而这个窄带与通常的S-N曲线相似，因此又将这个窄带称之为主S-N曲线，换句话说，它可以用一条数学上的S-N曲线有效地替代以前的多条S-N曲线族。

关于在ΔS_s-N图中结构应力范围的实际斜率，在考察了大量关于焊接接头的疲劳数据之后发现，所有的S-N数据都可以通过裂纹扩展指数m≈3.6很好地联系起来。

表6-1还给出了不同概率分布下的主S-N曲线试验统计常数^[3]，这些数据被进一步推广应用之前，人们又投入了大量的精力来验证主S-N曲线参数的正确性。这些验证数据涵盖了汽车工业、石化工业、海上船舶以及核工业等各种工程领域，验证的结果证明了这些参数是可靠的。

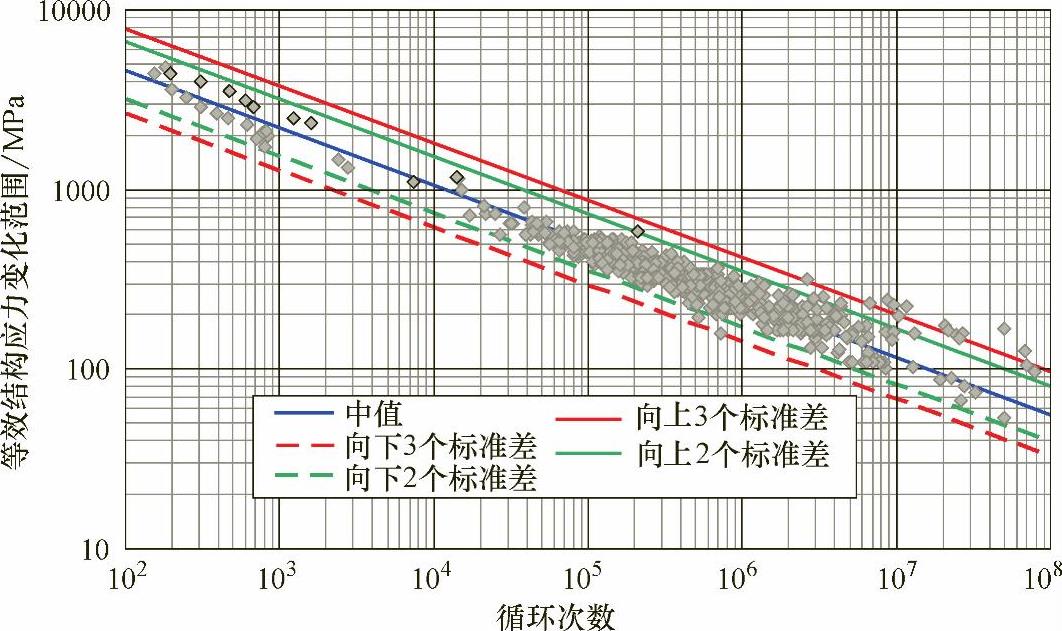
图6-8 主S-N曲线试验数据

表6-1 主S-N曲线参数表（钢材）

因此在2007年，这些数据经大批专家严格论证之后被写进美国ASME BPVC ⅤⅢ-2-2007的标准里。目前，主S-N曲线的数据又得到了进一步的丰富，例如包括铝焊接接头的主S-N曲线数据，在腐蚀环境下焊接接头的主S-N曲线数据，以及对焊缝进行各种不同工艺处理的主S-N曲线数据等。

最后还要讨论一下焊接残余应力与主S-N曲线方程的关系。在计算疲劳寿命的公式中可看出等效结构应力是关键因素，而残余应力的影响已经包含在主S-N曲线数据里，所以残余应力的存在并不会对焊接结构的疲劳寿命计算产生根本性影响。